How to Construct Parallel Lines
Learning how to construct parallel lines using only a compass and a straightedge is the goal of this lesson.
In this lesson, we will just show you how to construct a line that will be parallel to another given line. Here is how to do it!
Construct a line m that is parallel to a given line n and through a given point P that is not on the line.
Given: Line n and point P not on n. This is shown in the figure below

Construct: Line m through P with m || n
Step 1
Label two points R and S on n and draw the line RP.
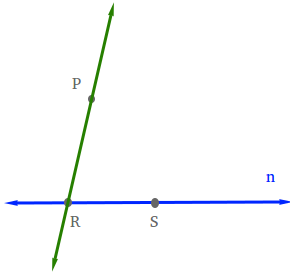
The Goal:
Construct an angle with vertex at P so that the angle is congruent to angle SRP.
What you are basically doing in the following steps is copying angle SRP using line RP. If you do not remember how to copy an angle, you can review this lesson about copying an angle.
In a nutshell, here is what you need to do.
Step 2
First, get a compass and set the opening to a distance that is less than the length of RS. Put the needle of the compass at point R. Then draw an arc that will cross line n and line PR. The arc will intersects line n and line PR at the two red dots.
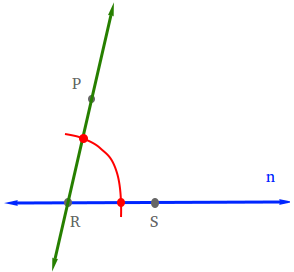
Step 3
Set the opening of the compass so that it still has the same distance that was used in step 2 to draw the red arc. Put the needle of the compass at point P and draw an arc.This arc intersects line PR at the yellow dot.
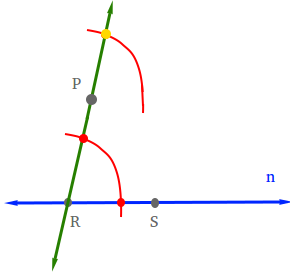
Step 4
Use the compass to measure the distance between the two red dots. You can do this by putting the needle of the compass at one of the red dot and the pencil at the other red dot.
Step 5
Using the distance you found in step 4, put the needle of the compass at the yellow dot and draw an arc (shown in black). Finally, draw the line between point P and the intersection of the black arc and the red arc. Let x be the name of the angle with vertex P.
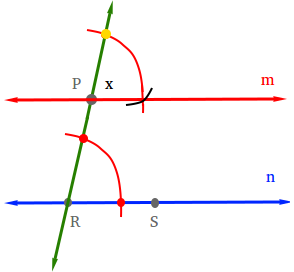
Line m is parallel to line n because angle x and angle SPR are corresponding angles that are equal. When corresponding angles are equal, the lines are parallel.