Inclination of a line
The inclination of a line or angle of inclination is the acute or obtuse angle that is formed when a nonhorizontal line intersects the x-axis.
Formal definition:
The inclination of a nonhorizontal line is the positive angle θ with θ less than 180 degrees and measured counterclockwise from the x-axis to the line.
In the figure below, there are two angles. However, the angle in blue is the angle of inclination since it is measured counterclockwise according to the definition. We see that the slope is positive.
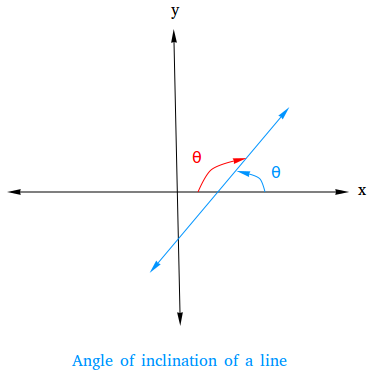
When the slope is positive, the angle of inclination is an acute angle.
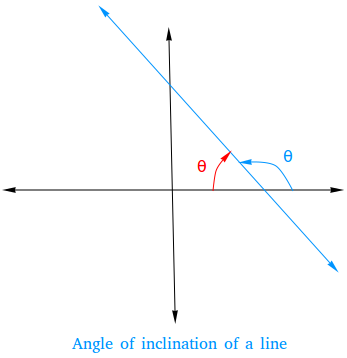
In the figure
above, you can again see that there are two angles. The angle in blue is once again the angle of
inclination since it is measured counterclockwise according to the
definition.
Notice though that this time the angle is bigger than 90 degrees and the slope is negative.
When the slope is negative, the angle of inclination is an obtuse angle.
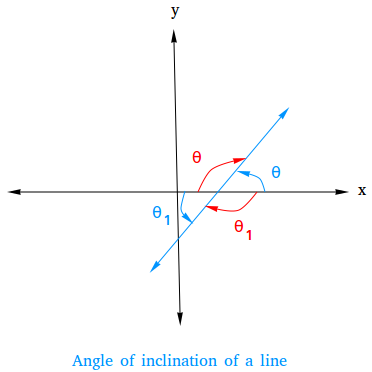
Notice also that when a line intersects with the x-axis, 4 angles are formed as shown below.
However
the angles in blue are vertical angles and therefore have the same
measure. By the same token, the angles in red are vertical angles and
also have the same measure. Therefore, we only need to concern ourselves
with θ and θ
θ is not the angle of inclination, so we are left with θ
The relationship between the slope of a line and its inclination is given by the following equation.
m = tan θ
How to derive the equation relating the inclination of a line to the slope (m = tan θ)
Slope is positive
Consider the following figure. Point (x1, 0) intersects the x-axis and (x2, y2) is another point on the line.
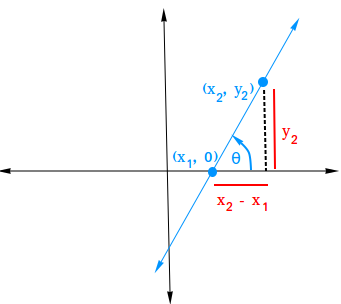
If m = 0, θ = 0 since the line is horizontal. Therefore, the result is true for horizontal lines since m = 0 = tan 0.
If the line has a positive slope, then
Combining equation I and equation II, we get m = tan θ
Slope is negative
Consider the following figure. Point (x1, 0) intersects the x-axis and (x2, y2) is another point on the line.
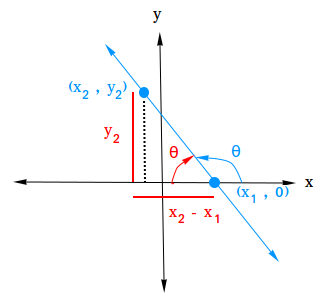
Key concept: θ is the reference angle for θ
Therefore, sin(θ) = sin(θ)
for example, sin (120 degrees) = sin(60 degrees) = 0.8660254038
If sin(θ) = sin(θ), then tan(θ) = tan(θ)
m = tan θ
Exercises on how to find or calculate the angle of inclination
1) When the line is vertical, the inclination of a line is 90 degrees. In this case, there is no answer for the slope.
2) When the line is horizontal, the inclination of a line is 0 degree.
3) Find the slope when the inclination of a line is 45 degrees
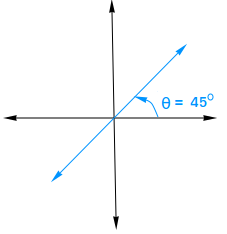
m = tan θ = tan 45 degrees
Type 45 degrees and use the tan key on a scientific calculator.
You will see that tan (45 degrees) = 1
m = 1
Now suppose, you are given a slope of 1 and want to find the angle of inclination.
θ = tan-1(1)
Type 1 and use the tan-1 key on a scientific calculator.
You will see that θ = tan-1(1) = 45 degrees
4) Find the slope when the inclination of a line is 135 degrees
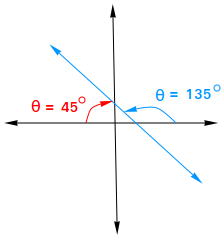
m = tan θ = tan 135 degrees
Type 135 degrees and use the tan key on a scientific calculator.
You will see that tan (135 degrees) = -1
m = -1
Now suppose, you are given a slope of -1 and want to find the angle of inclination.
Find tan-1(-1)
Type -1 and use the tan-1 key on a scientific calculator.
You will see that tan-1(1) = -45 degrees
As you can see -45 degrees is not the 135 degrees angle we started with.
To get 135 degrees, you need to add 180 degrees to 45 degrees.
When the slope is negative, θ = 180 degrees + tan-1(-1) = 180 degrees + 45 degrees = 135 degrees
For more exercises, check this website