Angle between two lines

Finding the angle between two lines using a formula is the goal of this lesson. When two lines intersect in a plane, their intersection forms two pairs of opposite angles called vertical angles.

If the two lines are not perpendicular and have slopes m₁ and m₂, then you can use the following formula to find the angle between the two lines.

$$ tan \ θ = \left\lvert \frac{m_2 - m_1}{1 + m_1m_2} \right\rvert $$

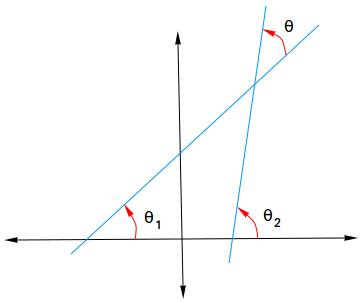
How to derive the formula to find the measure of the angle between two lines

First, notice that when two lines intersect, one of the two pairs is acute and the other pair is obtuse.  The angle between two lines is defined as the smallest of these angles or the acute angle denoted by θ.

We are going to use the inclinations of the two lines to find the angle between the two lines. You may need to review the lesson about inclination of line.

Second, we need to show that θ = θ₂ - θ₁

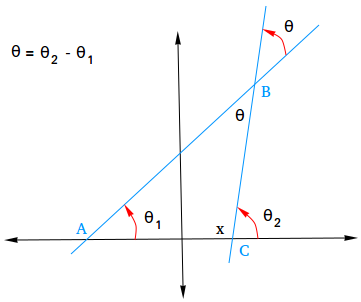
Using triangle ABC, we know that the sum of the angles in that tiangle is equal to 180 degrees.

θ + θ₁ + x  = 180 (equation 1)

Furthermore, x + θ₂  = 180 (equation 2) since x and θ₂  form a straight line.

Replace 180 with x + θ₂ in equation 1.

We get θ + θ₁ + x  = x + θ₂

Subtract x from both sides

θ + θ₁ + x - x = x - x + θ₂

θ + θ₁ =  θ₂

Subtract θ₁ from both sides

θ + θ₁ - θ₁  =  θ₂ - θ₁

θ  =  θ₂ - θ₁

Now, you can use the formula for the tangent of the difference of two angles.

tan θ = tan ( θ₂ - θ₁)

Third, in the lesson about inclination of a line, we learned that tan θ = m

Thus, tan θ₁ = m₁ and tan θ₂ = m₂

After substituting m₁ for tan θ₁ and m₂ for tan θ₂ in the equation immediately above, we get:

Notice the use of the absolute value to ensure that tan θ is equal to a positive number.

Exercises about finding the angle between two lines

1) Find the angle between the following two lines.

Line 1: 3x -2y = 4

Line 2: x + 4y = 1


Solution

Put 3x - 2y = 4 into slope-intercept form so you can clearly identify the slope.

3x - 2y = 4

2y = 3x - 4

y = 3x / 2 - 4/2

y = (3/2)x - 2

Put x + 4y = 1 into slope-intercept form so you can clearly identify the slope.

x + 4y = 1

4y = -x + 1

y = -x/4 + 1/4

y = (-1/4)x + 1/4

The slopes are 3/2 and -1/4 or 1.5 and -0.25. It does not matter which one is m₁ or m₂. You will get the same answer.

Let m₁  = 1.5 and m₂ = -0.25

θ = tan^-1(2.8) = 70.35 degrees

2) Find the angle between the following two lines.

Line 1: x - 4y + 4 = 0

Line 2: 3x - 4y - 8 = 0


Solution

Put x - 4y + 4 = 0 into slope-intercept form so you can clearly identify the slope.

x - 4y + 4 = 0

4y = x + 4

y = x / 4 + 4/4

y = (1/4)x + 1

Put 3x - 4y - 8 = 0 into slope-intercept form so you can clearly identify the slope.

3x - 4y - 8 = 0

4y = 3x - 8

y = 3x/4 - 8/4

y = (3/4)x - 2

The slopes are 3/4 and 1/4 or 0.75 and 0.25. Again, it does not matter which one is m₁ or m₂. You will get the same answer.

Let m₁  = 0.75 and m₂ = 0.25

tan θ = |-0.4211| = 0.4211

θ = tan^-1(0.4211) = 22.84 degrees