Introduction to matrices

To start off our introduction to matrices, we will first show you that a matrix is nothing but a convenient way to organize data with rows and columns.

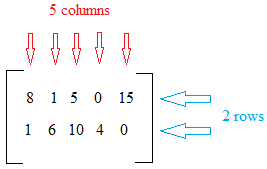
Suppose you have a business selling T-shirts and pants. The table below shows the number of items sold for 5 days.

	Monday	Tuesday	Wednesday	Thursday	Friday
T-shirt	8	1	5	0	15
Pants	1	6	10	4	0

You may re-organize the number of T-shirts and pants sold from Monday through Friday using the matrix below.

8	1	5	0	15
1	6	10	4	0

The matrix above has 2 rows and 5 columns and we say the matrix is a 2 × 5 matrix.

2 × 5 is read 2 by 5. It does not mean multiplication.

Notice that the number of rows is listed first and that is the way it goes with matrices.

2 × 5 is called the dimensions of the matrix.

If 4 × 3 represent the dimensions of a matrix, the matrix has 4 rows and 3 columns.

We use a capital letter such as A, B, or C to represent a matrix as shown below:

A =

8	1	5	0	15
1	6	10	4	0

Each number in a matrix is a matrix element. We like to locate the position of elements when working with matrices.

To Locate elements for matrix A, use a lower case letter and a subscript with two numbers.

The number on the left of the subscript represents the row the element is located.

The number on the right of the subscript represents the column the element is located.

a₂₃ is the element in the second row and third column.

a₂₃ = 10

a₁₅ is the element in the first row and fifth column.

a₁₅ = 15

Don't let the 15 confuse you. The number in the first row and fifth column does not have to be 15. It could be anything.

Let's us re-organize the information!

	T-shirt	Pants
Monday	8	1
Tuesday	1	6
Wednesday	5	10
Thursday	0	4
Friday	15	0

As a matrix, we can write B =

8	1
1	6
5	10
0	4
15	0

The dimension of matrix B is 5 × 2

Important concepts: Although matrices A and B are describing the same situation, the matrices are not equal.

Two matrices are equal when they have the same dimensions and equal corresponding elements.

Simply put, write down a matrix and then write down again the exact same matrix. These two matrices are equal!