Probability of independent events

In this lesson, we will do the following using a table that shows test results for 200 students who took a GED test.

• Compute the probability of independent events and show the relationship between independent events and their probabilities

• Compute the probability of dependent events and show the relationship between dependent events and their probabilities

• Explain the difference between independent events and dependent events

Let us start with the probability of independent events. Consider the following table.

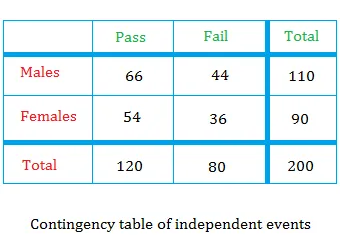
Let pass be the event that a randomly selected student has passed the test

Let male be the event that a randomly selected student is male.

Compute  these two probabilities: P(pass) and P(pass / male)

We notice that P(pass) = P(pass / male)

This means that the probability to pass is the same as the probability to pass if the student is male.

In other words, it does not matter if the student is male, the passing rate is still the same.

Passing does not depend on the gender.

We can then conclude that the two events  " pass "  and  " male " are independent events. Neither event will influence the other.

Since passing does not depend on gender, you should also get 0.60 when we compute P(pass) and P(pass / female)

What about the result shown in the table in the lesson about marginal probability?

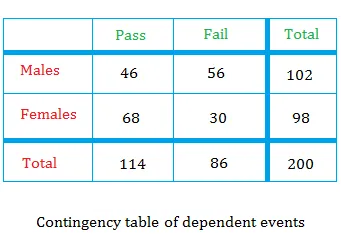
Notice that adding the event " male ", changed the probability.

Since the event " male " changed the probability, the two events " pass "  and  " male " are dependent events.

By the same token, the two events " pass "  and  " female " are dependent events.

Notice below what P(pass / female) gives!

Since 0.69 is bigger than 0.45, females are more likely to pass the test than males.

For this result, passing here depends on the gender.