Least Common Multiple
The least common multiple (LCM) is the smallest number that is a multiple of two numbers. The interactive lesson below will help you explore the best 3 methods for finding the least common multiple with unlimited practice. My favorite is method #1, which I learned when I was in school!
Interactive Lesson Showing how to Find the Least Common Multiple
What are Multiples?
An understanding of multiples is important in order to understand the meaning of LCM. When a number is multiplied by different whole numbers, the resulting products are multiples of that number.
How to Find the Multiples of a Number
The multiples of a number are the answers that you get when you multiply that number by the whole numbers except 0.
Remember that the whole numbers are all numbers from 0 to infinity.
Whole number = {0, 1, 2, 3, 4, 5, 6, 7, 8, ...}
So multiply any number by 1, 2, 3, 4, 5, 6, 7, 8, ... to get the multiples of that number.
- For instance, you get the multiples of 4 by multiplying 4 by 1, 2, 3, 4, 5, ...
- I put the dots to show that the sets of whole numbers continues forever.
- The answer is { 4, 8, 12, 16, 20, ...}
- In the same way, the multiples of 9 are all the numbers that you get when you multiply 9 by 1, 2, 3, 4, 5, 6, ...
- I put the dots to show that the sets of whole numbers continues forever.
- After you do that, you will get { 9, 18, 27, 36, 45, 54, ...}
How to Find the Least Common Multiple
The LCM of two numbers is the smallest number that is a multiple for both numbers.
Method #1: Set Intersection Method
Example: Find LCM of 6 and 9.
First list all the multiples of 6.
- You get {6, 12, 18, 24, 30, 36, 42, 48, 54, 60,....}
Next, list all the multiples of 9.
- You get {9, 18, 27, 36, 45, 54, 63, 72, 81, 90....}
Pull out all the common multiples or find the intersection of the two sets.
- The common multiples are {18, 36, 54, ...}
Looking at the list of common multiples immediately above, you can see that the smallest number that is a multiple of both 6 and 9 is 18.
Of course, 36 is also a common multiple of 6 and 9. However, it is not the smallest common multiple.
Example: Find LCM of 2 and 3.
- Multiples of 2 are {2, 4, 6, 8, 10, ...}
- Multiples of 3 are {3, 6, 9, 12, 15, ...}
- The least common multiple of 2 and 3 is 6.
You can also write LCM(2,3) = 6 .
Method #2: My Teacher's Method
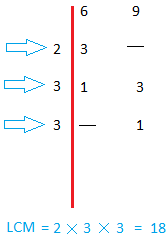
Find LCM( 6, 9) and LCM (120, 180)
Technique:
Start by dividing each number by 2. (If 2 does not work, start with 3 instead, and so forth ...)
Keep dividing by 2 until 2 does not work anymore.
When 2 does not work anymore, divide by 3.
When 3 does not work anymore, divide by 4.
Keep doing this until you can no longer divide.
LCM = The product of all the numbers on the left of the red line.
 |
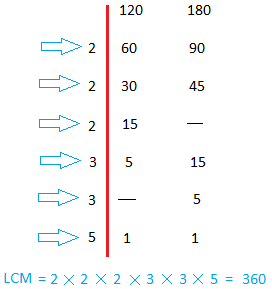 |
Find LCM(120, 180)
First, find the prime factorization of the numbers.
120 = 12 × 10 = 2 × 2 × 3 × 2 × 5 = 23 × 31 × 51
180 = 18 × 10 = 2 × 3 × 3 × 2 × 5 = 22 × 32 × 51
The least common multiple will be 2x × 3y × 5z
x is the bigger exponent of 23 and 22
y is the bigger exponent of 31 and 32
y is the bigger exponent of 51 and 51
The least common multiple is 23 × 32 × 5 = 2 × 2 × 2 × 3 × 3 × 5 = 360