Math problem solving strategies your teacher may have never shown you.
Some math problem solving strategies will be considered here. Study them carefully so you know how to use them to solve other math problems.The biggest challenge when solving math problems is not understanding the problem.- Make a guess and test it
- Make a list
- Use a variable
- Draw a diagram
- Working backward
Among the math problem solving strategies, sometimes, you need to make a guess and test it
Example #1 The sum of 2 consecutive odd numbers is 44. What are the two integers?
Before guessing, always make sure you understand the problem. If possible, get a dictionary or look up the vocabulary words in your math textbook.
Sum: refer to adding numbers
consecutive: In the context of this problem, it will mean that we are looking for an odd number and the next odd number that immediately follows the first one.
Guessing here means that you will arbitrarily pick two odd numbers, add them, and see if it is equal to 44.
15 + 17 = 32. It does not work. Since 32 is smaller than 44, pick higher numbers.
19 + 21 = 40. Getting closer
21 + 23 = 44. Here we go. We found the two numbers by guessing!
Example #2
A kindergarten class is going to a play with some teachers. Tickets cost 5 dollars for children and 12 dollars for adults. Number of tickets sold amount to 163 dollars. How many teachers and children went to the play?
First, make sure you understand the problem. What the problem is really asking is the following:
How many adult tickets were sold? How many children tickets were sold?
Guess and check!
Pretend that 3 children tickets were sold. Then, 17 adult tickets were sold
Total cost = 3 × 5 + 17 × 12 = 15 + 204 = 219
The total is too high. Pretend that 14 children tickets were sold. Then, 6 adult tickets were sold.
Total cost = 14 × 5 + 6 × 12 = 70 + 72 = 142
The total is a little too low now. Pretend that 12 children tickets were sold. Then, 8 adult tickets were sold.
Total cost = 12 × 5 + 8 × 12 = 60 + 96 = 156
As you can see, it is going higher again and it is getting closer to 163. May be 11 tickets for children and 9 tickets for adults will work.
Total cost = 11 × 5 + 9 × 12 = 55 + 108 = 163
Here we go! 11 children and 9 teachers went to the play.
Solving a math problem by making a list
This could happen if I slightly modify example #2Example #3
A kindergarten class is going to a play with some teachers. Tickets cost 5 dollars for children and 12 dollars for adults. A total of 20 people could go to the play. There must be at least 2 teachers to supervise the children, but no more than 10. Find all possible ways this could be done. How can the school minimize their cost?
This problem involves making a list
If 2 teachers go, then 18 children will go
If 3 teachers go, then, 17 children will go
and so forth...
Total cost = 2 × 12 + 18 × 5 = 24 + 90 = 114
Total cost = 3 × 12 + 17 × 5 = 36 + 85 = 121
Total cost = 4 × 12 + 16 × 5 = 48 + 80 = 128
Total cost = 5 × 12 + 15 × 5 = 60 + 75 = 135
Total cost = 6 × 12 + 14 × 5 = 72 + 70 = 142
Total cost = 7 × 12 + 13 × 5 = 84 + 65 = 149
Total cost = 8 × 12 + 12 × 5 = 96 + 60 = 156
Total cost = 9 × 12 + 11 × 5 = 108 + 55 = 163
Total cost = 10 × 12 + 10 × 5 = 120 + 50 = 170
As you can see, the less teacher they send, the less the cost.
The least expensive case is to send 2 teachers and 18 children. Other teachers will not be happy about it
Judy and Ramey together have 42 animals. Judy has 12 fewer animals than Ramey. How many stuffed animals does each girl have?
Again, you could make a list if you look for all combinations of 2 numbers to add to get 42 and then choose the pair with a difference of 12.
42 = 41 + 1 difference is 40
42 = 40 + 2 difference is 38
42 = 39 + 3 difference is 36
42 = 38 + 4 difference is 34
42 = 37 + 5 difference is 32
42 = 36 + 6 difference is 30
42 = 35 + 7 difference is 28
42 = 34 + 8 difference is 26
42 = 33 + 9 difference is 24
42 = 32 + 10 difference is 22
42 = 31 + 11 difference is 20
42 = 30 + 12 difference is 18
42 = 29 + 13 difference is 16
42 = 28 + 14 difference is 14
42 = 27 + 15 difference is 12
Stop! You have found what you are looking for.
The numbers are 27 and 15.
27 - 15 = 12
27 + 15 = 42
So Ramey has 27 stuffed animals and Judy has 15.
Math problem solving strategies could also make use of a variable.
Example #4The use of a variable means that you will let the unknown be x, write and equation, and solve the equation.
Use of a variable for example #3
Let x be number of children tickets. Then, 20 - x is number of adult tickets
cost of children tickets + cost of adult tickets = total cost
x × 5 + (20 - x ) × 12 = 163
5x + 20 × 12 - x × 12 = 163
5x + 240 -12x = 163
5x + 240 -240 -12x = 163 - 240
5x - 12x = -77
-7x = -77
-7x/-7 = -77/-7
x = 11.
Among all math problem solving strategies, my favorite is draw a diagram.
Example #5A highway has a gas station every 2 miles, a rest area every 4 miles, and a Burger King every 3 miles. Where is the closest gas station, rest area, and burger king all at the same time?
A little diagram describing the situation is all we need to tackle this problem real quick.
Let red be gas station, let blue be rest area, and let green be Burger King. Draw the diagram below.
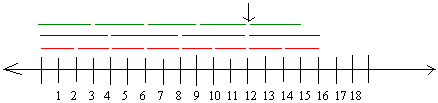 |
Notice that every gap between the red lines represents the location of a gas station. Same idea for the blue lines and the green lines
The vertical arrow is point toward the location where all 3 services can be found at the same time.
As you can see, it is 12 miles!
You may wonder. How do we get the answer without drawing a diagram? Great question! That will be important if you are dealing with big numbers.
To get the 12, you need to look for the Least common multiple (LCM). The smallest number that is a multiple of 2, 3, and 4
That number is indeed 12. More information on Least common multiple
Among great math problem solving strategies, is the one when you work backward
Example #6One day, I woke up and feeling generous, I took all the apples in my refrigerator and I decided to give them away.
I went outside and I gave one-half of my apples plus one to the first stranger I met. Then, I gave one-half of the remaining apples plus one to the second person I met and one-half of the remaining apples plus one to the third person. I had one apple left at the end. How many apples did I have when I left my house (This is not a true story. I made that up)
Starting backward means that you are starting with the result and work your way backward until you get what you started with.
Third person: received one-half plus one. Just do the reverse of that. Give yourself one and twice.
1 + 1 = 2 and 2 × 2 = 4. ( This makes sense because giving one-half of 4 plus one means giving 2 and then 1)
Second person: received one-half plus one. Just do the reverse of that. Give yourself one and twice.
4 + 1 = 5 and 5 × 2 = 10.
First person: received one-half plus one. Just do the reverse of that. Give yourself one and twice.
10 + 1 = 11 and 11 × 2 = 22.
So you had 22 apples in your bag.
The math problem solving strategies I discussed above are great examples. Make sure you understand them. Hope you had fun exploring these math problem solving strategies!