Multiplying Integers

Multiplying integers is just like the multiplication of whole numbers, except that with integers, you have to keep tract of your signs.

Recall that 6 + 6 + 6 = 6 × 3

Instead of adding 6 three times, you can multiply 6 by 3 and get 18, the same answer.

Similarly,

6 + 6 + 6 + 6 + 6 + 6 + 6 = 6 × 7 = 42

Still by the same token,

2 + 2 + 2 + 2 = 2 × 4

In algebra, 2 × 4 can be written as (2)(4)

You can think of this as four groups of 2.

This situation is shown in the number line below.

You basically start at 0 and count by 2's until you have put four 2's on the number line. You end up at 8 and 8 is positive.

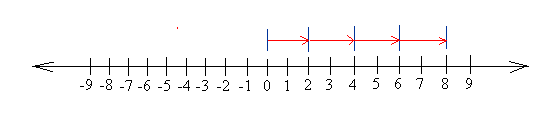Representation of 2 times 4

Notice that 2 and 4 are positive.

In general,when multiplying integers, remember the followings:

Positive × Positive = Positive

For example,

7 × 6 = 42

2 × 5 = 10

3 × 10 = 30

8 × 2 = 16

Now, try adding -3 to -3

- 3 + -3 = -3 × 2

The reasoning is the same; Instead of adding -3 two times, you can just multiply -3 by 2.

To model this on the number line, just start at 0 and put 2 groups of -3 on the number line. You end up at -6 and -6 is negative.

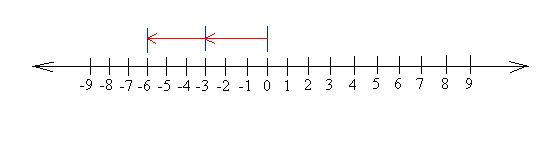Representation of -3 times 2

Notice that -3 is negative and 2 is positive.

In general,

Negative × Positive = Negative

For example:

-8 × 5 = -40

-6 × 5 = -30

-4 × 2 = - 8

-3 × 4 = - 12

Now what about 3 × -2 ?

Start at 0 and put three groups of - 2 on the number line and you will end up at -6 as shown below:

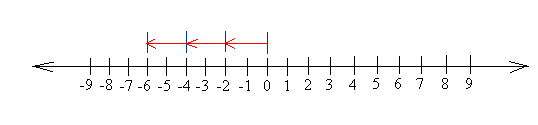Representation of 3 times -2

Notice that this time 3 is positive and -2 is negative, yet we still get -6.

In general,when multiplying integers

Positive × Negative = Negative

For example:

8 × -5 = - 40

2 × -10 = -20

3 × - 6 = - 18

5 × -5 = - 25

The last case we need to cover is:

Negative × Negative = ?

This case cannot be shown on a number line.

In general, when multiplying integers, 

Negative × Negative = Positive

For example:

-9 × -5 = 45

-4 × -2 = 8

-1 × -1 = 1

-2 × - 6 = 12

However, why is a negative times a negative equal a positive?

We will use proof by contradiction to prove it.

In math, when doing a proof by contradiction, you will suppose that the hypothesis is false and show that making this assumption will lead to a contradiction or something that does not make any sense.

At this point, please do not shake in your boots! If you accept that a negative times a negative is a positive, skip the following. If not, proceed!

Here is the proof:

Suppose that -2 × - 5 = -10

-10 is negative, so we made the assumption that the answer is negative, but not positive.

Next, divide both sides of your equation ( -2 × -5 = -10) by -5.

We get:

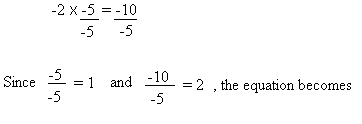
-2 × 1 = 2

-2 = 2

Since -2 is never equal to 2, we have found a contradiction.

Therefore, The assumption that -2 × -5 = -10 is false.

We must have -2 × -5 = 10.

Notice that -5 divided by -5 is 1 because -5 × 1 = -5 or -5 goes into -5 once.

-10 divided by -5 is 2 because -5 × 2 = -10 or -5 goes into -10 twice.

The proof above is not a real proof because it takes into consideration specific numbers. A good proof is always generic. A generic proof is beyond the scope of this topic, so let us be happy with the one above at least for now.

To sum up, here is the big picture when multiplying integers :

Multiplying integers quiz to check how well you understand this lesson