Number of segments

Our goal with this lesson is to derive a formula for the number of segments between n points.

To derive the formula, our strategy will be to see how many segments can be formed with 2, 3, 4, or 5 points.

Then, we will try to identify a pattern that can help us derive the formula

How many segments can be formed with 2 points?

This is an easy question. We can get one segment



How many segments can be formed with 3 points?

I recommend not putting the 3 points on the same line. It will be easier to keep track and count the segments

Put the points on a piece of paper as shown below:

It is still easy to see that we can make 3 segments with 3 points

How many segments can be formed with 4 points? Again, do not put the points on the same line

Caution:

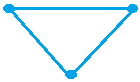
Usually people have no difficulties showing the 4 segments in blue. However, many people forget the two segments in red

So, 6 segments can be drawn with 4 points

How many segments can be formed with 5 points?

Things start getting a little complicated here. I will show you a way to count so you don't miss or overlook any segment

Keep in mind that the way I arrange the points is the way I believe will make it easier to count especially when you start counting the number of segments you can get with 5, 6, or 7 points

First, you can make these quick 5 segments that are shown in blue

Then, from each vertex, draw all the possibles diagonals

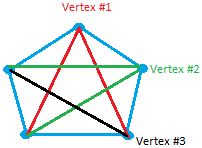
I am using a different color and a numbering system so you can clearly see

You can get two more from vertex #1 shown in red, 2 more from vertex #2 shown in green, and 1 more from vertex #3 shown in black

So 10 segments can be drawn with 5 points



Let us organize our findings. The table below will show you what we got so far and a math behind it

2 points	1 segment   =   2 × 1 / 2
3 points	3 segments   =   3 × 2 / 2
4 points	6 segments   =   4 × 3 / 2
5 points	10 segments   =   5 × 4 / 2
n points	n × ( n -1 ) / 2 segments

Explanations:

The denominator is always 2, so 2 will be the denominator in the general formula

The numerator has two numbers. The number on the right side of the multiplication is always 1 less the one on the left

That is why if the number on the left is n, the one on the right is n - 1

What does n represent? Look carefully and you will see that it represents the number of points

Now that you have a formula, you can even calculate the number of segments you can get with 25 points if you like



It is very useful to get a formula to get the number of segments with lots of points such as 25

If you tried to do the drawing above, things will get very messy