Perimeter of a square

The perimeter of a square is the distance around the square. In other words, the perimeter is the sum of the lengths of its sides. Since the sides of a square are all equal, you can just multiply the length of one side by 4 to get the perimeter.

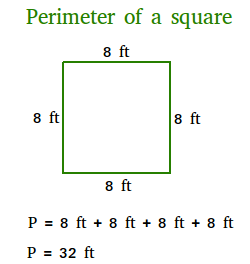
Derivation of perimeter of square formula

The perimeter is expressed in units.

• If s is measured in feet, then the perimeter is measured in feet or ft.

• If s is measured in centimeters, then the perimeter is measured in centimeters or cm. 

• If s is measured in meters, then the perimeter is measured in meters or m.

How to find perimeter of square

It all depends on which information is given to you. You could find the perimeter of a square using one of the following informations.

• The length of one side 
• The area of the square
• The diagonal of the square

How to find the perimeter of a square using the length of one side of the square

Example #1

Find the perimeter of a square when s = 3 cm

P = 4 × s = 4 × 3 = 12 cm

Notice that it is perfectly ok to do P = 3 + 3 + 3 + 3 = 12

However, it is usually easier and quicker to do 4 times 3 than adding 3 four times.

Example #2

Find P when s = 5 cm

P = 4 × s = 4 × 5 = 20 cm

Example #3

Find P when s = 2/8 cm

P = 4 × s = 4 × 1/8

P = (4/1) × (2/8)

P = (4 × 2) / ( 1 × 8 ) = 8 / 8 = 1 cm

How to find the perimeter of a square using the area of the square

Example #4

The area of a square is 36 square meters. What is the perimeter of the square?

The first thing to do is to find the side length of the square by taking the square root of the area.

The formula to find the area of a square is A = s² 

Substitute 36 for A.

36 = s²

s = √(36)

s = 6

P = 4 × 6 = 24 meters

How to find the perimeter of a square using the length of the diagonal of the square

Example #5

If the diagonal of a square measures 2√2, find the perimeter.

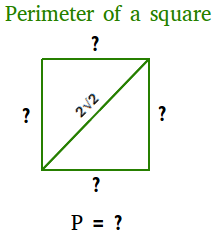
Notice that the length of the diagonal is the length of the hypotenuse. Therefore, use the Pythagorean theorem to find the length of the side of the square. Let s be the length of one side.

(2√2)² = s² + s²

2²(√2)² = 2s²

4(2) = 2s²

Divide both sides by 2

4 = s²

s is equal to square root of 4

s = 2

P = 4 × s

P = 4 × 2 = 8 

Finding the length of a side of a square when the perimeter is given

Example #6

A square has a perimeter of 12 inches. Find s

Here, given the perimeter, you are asked to find the length of a side of the square.

We know that P = 4 × s

You should replace P by 12 because that is what they gave you.

So, 12 = 4 × s

The problem becomes a multiplication equation that you need to solve

However you can solve this equation with mental math. Replace s by a question mark (?) and ask yourself the following:

4 times ? = 12 or 4 times what will give me 12? The answer is 3, so s = 3

Example #7

The perimeter of a square is 64 cm. What is the length of one side?

Again, since P = 4 × s, we get 64 = 4 × s after replacing P by 64.

Ask yourself 4 times what will give me 64? Since 4 times 16 is 64, s = 16

You can also solve the equation to find s. Just divide both sides of the equation by 4.

64 = 4 × s

64 / 4 = (4 × s) / 4

16 = s

Can the area and perimeter of a square be the same?

No, that is not possible! The perimeter is expressed in units. However, the area is expressed in square units or unit² 

Therefore, units can never be equal to unit² just like 4 could never be equal to 4² 

If you measure the perimeter of your garden, it could be equal to the perimeter of someone else's garden. 

If you measure the area of your garden, it could be equal to the area of someone else's garden. 

However, it does not make sense to say that the perimeter of your garden could be equal to the area of someone else's garden. 

However, if you would like to ignore all logic and the fact that they cannot be equal, you could let s² = 4s and see what you get for s. 

s² = 4s

s² - 4s = 0

s(s - 4) = 0

s = 0 and s = 4

P = 4s = 4(4) = 16 units

A = s² = 4² = 4(4) = 16 unit²

However, 16 units is not equal to 16 unit²