Solving Multiplication Equations

When solving multiplication equations, these equations may have the form ax = c, bx = d, or cx = f, etc...

Recall that ax + b = c is a linear equation.Thus, the equation ax = c is also a linear equation with b = 0.You can solve ax = c in just one step.

ax = c

(a/a)x = c/a

(1)x = c/a

x = c/a

Solving multiplication equations: Here are three examples showing how to solve these equations.

Example #1: Solve the multiplication equation 6x = 18 using division.

You could also solve 6x = 18 by multiplying both sides of the equation by the reciprocal of 6. The reciprocal of 6 is 1/6.

6x = 18

(1/6)6x = 18(1/6)

(1/6)(6/1)x = (18/1)(1/6)

[(1×6)/(6×1)]x = (18×1)/(1×6)

(6/6)x = 18/6

1x = 3

x = 3

Example #2: Solve the multiplication equation 2x = 10 using division.

Again, you could also solve 2x = 10 by multiplying both sides of the equation by the reciprocal of 2. The reciprocal of 2 is 1/2.

2x = 10

(1/2)2x = 10(1/2)

(1/2)(2/1)x = (10/1)(1/2)

[(1×2)/(2×1)]x = (10×1)/(1×2)

(2/2)x = 10/2

1x = 5

x = 5

Before you look at example #3, I strongly encourage you to review multiplication and division of fractions.

Example #3: Solve the multiplication equation (2/5)x = 10 using division.

Study example #3 carefully and remember that anything divided by the same thing is 1. That is why 2/5 divided by 2/5 is 1. Also, it is perfectly OK to write 10 as 10/1 because anything divided by 1 gives you the same thing.

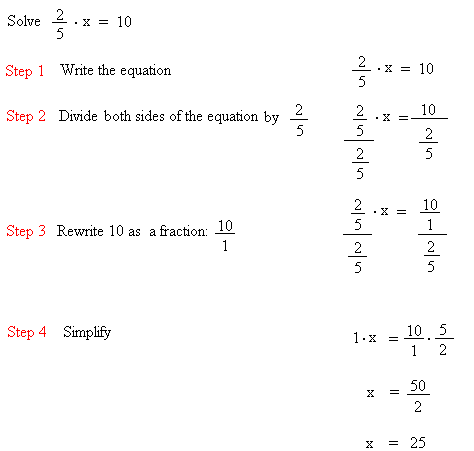
Now, you will see that it is easier to solve the equation (2/5)x = 10 when we multiply both sides of the equation by the reciprocal of 2/5.
The reciprocal of 2/5 is 5/2.

(5/2)(2/5)x = (5/2)10

(5/2)(2/5)x = (5/2)(10/1)

[(5×2)/(2×5)]x = (5×10)/(2×1)

(10/10)x = (50)/(2)

(1)x = 50/2

x = 25

---

Linear equations calculator
Easily solve equations of the form ax = c with the click of a button!