Perimeter of a trapezoid

The perimeter of a trapezoid where a, b, c, d are the lengths of its sides can be found using the formula p = a + b + c + d. Just like any other two-dimensional figures, the perimeter is just the sum of the lengths of the sides.

Example #1: Find the perimeter for the trapezoid below

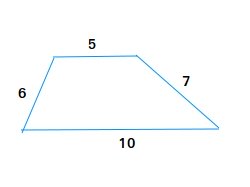
Perimeter  = 5 + 6 + 7 + 10 = 11 + 17 = 28

Now, let us make things a little bit more interesting. How about the figure below?

Example #2: Can you find the perimeter for this right trapezoid where ABC is a right triangle?

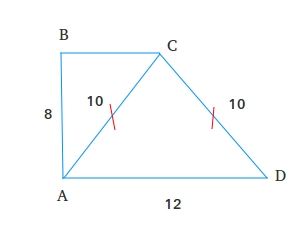
This example is a little tricky! Although 4 sides are given, one of them cannot be used to find the perimeter of the trapezoid. Can you tell which one? Yes, you guessed it right! The side that you cannot use is AC  = 10.

The sides that you can use are AB, AD, BC, and CD. However, we have another problem. BC is missing. We need to find BC.

BC is one side of the right triangle ABC. Therefore, we can use the Pythagorean theorem to find BC. 

AC² = AB² + BC²

10² = 8² + BC²

100 = 64 + BC²

100 - 64 = BC²

36 = BC²

Since 6² = 36, BC = 6

Perimeter = AB + BC + CD + AD  = 8 + 6 + 10 + 12 = 14 + 22 = 36

Finding the perimeter of a trapezoid when the height, the length of the top base, and the lengths of the nonparallel sides are given.

Example #3: Find the perimeter of the following trapezoid where the length of the bottom base is not known.

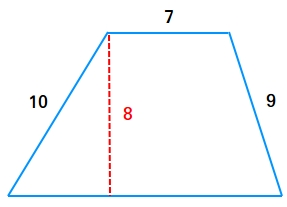
Make a rectangle by drawing a line from the other vertex on top. 

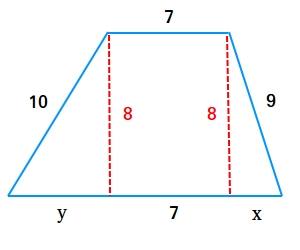
Now, once we find the length of x and the length of y, we can find the perimeter.

To find the length of y, we just need to use the Pythagorean theorem.

y² + 8² = 10²

y² + 64 = 100

y²  = 100 - 64

y²  = 36

Since 6² = 36, y = 6

Find x the same way.

x² + 8² = 9²

x² + 64 = 81

x²  = 81 - 64

x²  = 17

x  = √17 = 4.12

Perimeter = 6 + 7 + 4.12 + 9 + 7 + 10 = 43.12

Finding the perimeter of a trapezoid when the height, the length of the top base, and the bottom base angles are known.

Example #4: Find the perimeter of the following trapezoid where the length of the bottom base and the lengths of the nonparallel sides are not known.

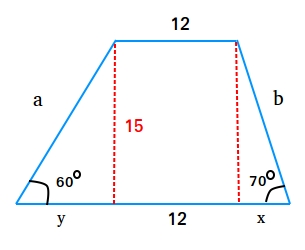
This time we may need to use some trigonometry to find the perimeter of this trapezoid.

To find a, b, x, and y, we can use trigonometric ratios.

sin(60 degrees) = 15/a or a  = 15/sin(60 degrees) = 15/0.866 = 17.3

tan(60 degrees) = 15/y or y  = 15/tan(60 degrees) = 15/1.732 = 8.66

sin(70 degrees) = 15/b or b  = 15/sin(70 degrees) = 15/0.94 = 15.95

tan(70 degrees) = 15/x or x  = 15/tan(70 degrees) = 15/2.74 = 5.47

Perimeter = 17.3 + 12 + 15.95 + 5.47 + 12 + 8.66 = 71.38

Finding the perimeter of an isosceles trapezoid in terms of x

Find the perimeter of an isosceles trapezoid if the length of the top base is equal to the length of the leg. Furthermore, the measure of one opposite angle is twice the other opposite angle. 

Let x  = length of top base = length of leg.

Take a look at the figure below so you understand the problem a little better.

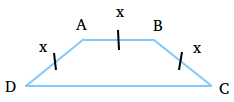
Here is what we know:

AB = x

AD = x

BC = x

We need to find DC 

Since the trapezoid is isosceles, we also know that ∠D = ∠C

Furthermore, ∠A +∠D = 180 degrees since the sum of interior angles on the same side of a transversal (AD in this case is the transversal) is equal to 180 degrees.

∠A is opposite to ∠C. Since ∠A is bigger than ∠C, then it is the one that is twice as big.

∠A = 2∠C

∠A = 2∠D (since ∠D = ∠C)

Substitute 2∠D for ∠A in ∠A +∠D = 180

2∠D +∠D = 180

3∠D = 180

∠D = 180/3 = 60

Draw the height of the trapezoid shown in red and then find the cosine of angle D.

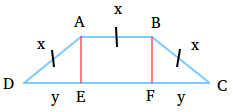
cos(∠D) = y/x  

cos(60 degrees) = y/x  

0.5 = y/x

Multiply both sides by x.

0.5x = y

y = DE = FC = 0.5x

Perimeter of the isosceles trapezoid = AB + BC + CF + FE + ED + DA  

Perimeter of the isosceles trapezoid = x + x + 0.5x + x + 0.5x + x = 5x