Area of a trapezoid

This lesson will show you how we find the area of a trapezoid using two different methods.

• Cutting up a trapezoid and rearranging the pieces to make a rectangle and a triangle.

• Using the formula for finding the area of trapezoids.

The first method will help you see why the formula for finding the area of trapezoids work.

Let us get started!

Draw a trapezoid on graph paper as shown below. Then, cut the trapezoid in three pieces and make a rectangle and a triangle with the pieces.

The figure on the left shows the trapezoid that you need to cut and the figure on the right shows the rectangle and 1 triangle. 

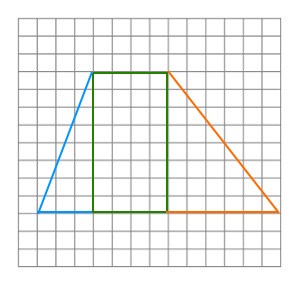
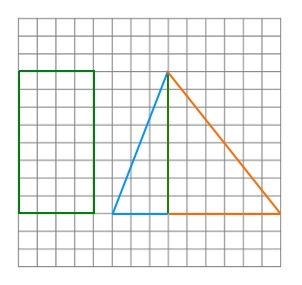
Then, we need to make the following four important observations.

1. 

Rectangle

Base = 4
Height = 8

2. 

Trapezoid

Length of bottom base = 13
Length of top base  = 4
Height = 8

3.

Newly formed triangle (made with blue and orange lines)

Length of base = 9 = 13 - 4 = length of bottom base of trapezoid - 4
Height = 8

4.

Area of trapezoid = area of rectangle + area of newly formed triangle.

Area of rectangle  =   base  × height = 4 × 8

Area of triangle     =  ( base  × height ) / 2

Area of triangle    =  [(13 - 4) × 8 ] / 2 = [13 × 8 + - 4 × 8] / 2

Area of triangle    = (13 × 8) / 2 + (- 4 × 8) / 2

Area of trapezoid = 4 × 8 + (13 × 8) / 2 + (- 4 × 8) / 2

Area of trapezoid = 8 × (4 + 13 / 2 + - 4 / 2)

Area of trapezoid = 8 × (4 - 4 / 2 + 13 / 2)

Area of trapezoid = 8 × (8 / 2 - 4 / 2 + 13 / 2)

Area of trapezoid = 8 × (4 / 2 + 13 / 2)

Area of trapezoid = (4 / 2 + 13 / 2) × 8

Area of trapezoid = 1 / 2 × (4 + 13 ) × 8

Let b₁ = 4 let b₂ = 13, and let h = 8

Then, the formula to get the area of trapezoid is equal to 1 / 2 × (b₁ + b₂ ) × h

Trapezoid area formula

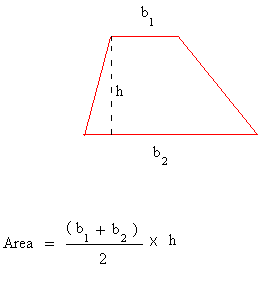
The area is expressed in square units.

• If the bases and the height are measured in meters, then the area is measured in square meters or m².

• If the bases and the height are measured in centimeters, then the area is measured in square centimeters or cm².

• If the bases and the height are measured in feet, then the area is measured in square feet or ft².

Examples showing how to find the area of a trapezoid using the formula

Example #1:

If b₁ = 7 cm,  b₂ = 21 cm, and h = 2 cm, find the area of the trapezoid 

Area = 1 / 2 × (b₁ + b₂ ) × h = 1 / 2 × (7 + 21) × 2 = 1 / 2 × (28) × 2

Area = 1 / 2 × 56 =  28 square centimeters or 28 cm²

Example #2:

If b₁ = 15 cm,  b₂ = 25 cm, and h = 10 cm, find the area of the trapezoid

Area = 1 / 2 × (b₁ + b₂ ) × h = 1 / 2 × (15 + 25) × 10 = 1 / 2 × (40) × 10

Area = 1 / 2 × 400 = 200 square centimeters or 200 cm²

Example #3:

If b₁ = 9 inches,  b₂ = 15 inches, and h = 2 inches, find the area of this trapezoid

Area = 1 / 2 × (b₁ + b₂ ) × h = 1 / 2 × (9 + 15) × 2 = 1 / 2 × (24) × 2

Area = 1 / 2 × 48 = 24 square inches or 24 in.²

Area of a trapezoid when the height is missing or not known

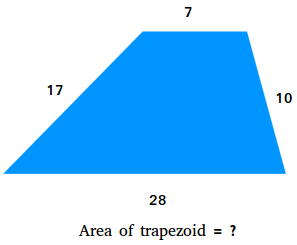
Suppose you only know the lengths of the parallel bases and the lengths of the legs of the scalene trapezoid shown above. How do you find the area? You need to make a rectangle and a triangle with the trapezoid.

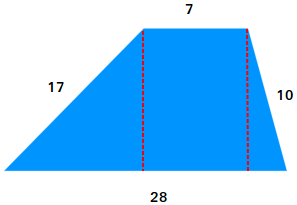
Cut the trapezoid into 3 pieces, a rectangle, and two right triangles. Then, bring together the two right triangles and make only 1 triangle. You will end up with a rectangle and a scalene triangle.

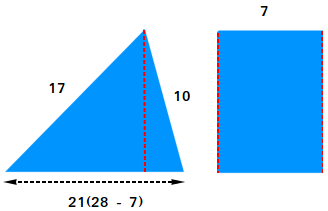
Use Heron's formula to find the area of the scalene triangle.

Area = √[s × (s − a) × (s − b) × (s − c)], s = (a + b + c)/2

a = 17, b = 10, and c = 21

s = (17 + 10 + 21)/2 = 48/2 = 24

s − a = 24 − 17 = 7

s − b = 24 − 10 = 14

s − c = 24 − 21 = 3

s × (s − a) × (s − b) × (s − c) = 24 × 7 × 14 × 3 = 7056

√(7056) = 84

Area of the scalene triangle = 84

Use the area of the scalene triangle to find the height of the triangle. Notice that the base of the triangle is 21 and the height h of the scalene triangle is also the missing side of the rectangle.

84 = (21 × height) / 2

168 = 21 × height

168 / 21 = height

Height = 8

Area of rectangle is 8 × 7 = 56

Area of trapezoid = area of the scalene triangle + area of rectangle = 84 + 56 = 140

Area of a trapezoid quiz to find out if you really understand this lesson.