Perpendicular bisector

A perpendicular bisector of a segment is a line, segment or ray that is perpendicular to the segment at its midpoint.

Therefore, a ⟂ bisector will bisect a segment into two congruent segments.


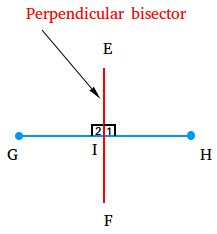
In the figure below, line EF is the ⟂ bisector of segment GH. Angle 1 and angle 2 are right angles. Segment GI is equal to segment IH. Therefore, I is the midpoint of segment GH.

You could also call the ⟂ bisector the locus of points equidistant from two given points.

This makes sense because when you are looking at the red line, you can see that every point on that line is equidistant to G and H.

Perpendicular bisector of a triangle

The perpendicular bisector of a side of a triangle is a line that bisects and is perpendicular to a side of the triangle.

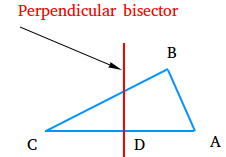
In the figure above, the red line is the ⟂ bisector of side CA.

Notice that the bisector does not necessarily bisects the triangle into two congruent figures.