Polynomial function
By definition, a polynomial function is a function that can be written as shown below:
f(x) = anxn + an-1xn-1 + ... + a2x2 + a1x1 + a0
You could also use p(x) instead of f(x) in order to be more precise.
p(x) = anxn + an-1xn-1 + ... + a2x2 + a1x1 + a0
Notice the following important conditions about a polynomial function
- n is a nonnegative integer or an integer that is either positive or zero
- The coefficients an , an-1 , ... , a2 + a1 , a0 are real numbers and they are constants
The terms in the polynomial function above are in descending order by degree
A polynomial is in standard form if the terms in the polynomial are in descending order by degree.
Notice that the exponents n, n-1, ... 2, 1 are whole numbers. If the exponent is negative, then it is not a polynomial.
Examples of polynomial functions
p(x) = 9x + 15
p(x) = x2 - 8
p(x) = x3 + 3x2 - x - 3
p(x) = -2x5 + 6x4 + 10x3 + -3x2 + 5x + 9
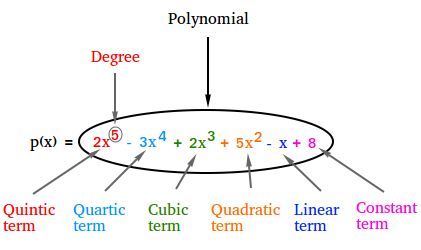
For the polynomial function p(x) = -2x5 + 6x4 + 10x3 + -3x2 + 5x + 9, notice how you can name each term of the function. This is important since it helps us to name and identify the different types of polynomial functions.
-2x5 is the quintic term
6x4 is the quartic term
10x3 is the cubic term
-3x2 is the quadratic term
5x is the linear term
9 is the constant term
The degree of a polynomial function is the biggest degree of any term of the polynomial. Therefore, the degree of the polynomial function above is 5.
The leading term is the term with the biggest degree. Therefore, the leading term of the polynomial function above is the quintic term or -2x5
The leading coefficient is the coefficient of the leading term. The leading coefficient is -2 then for the polynomial function above.
Types of polynomial functions
A constant function p(x) = c, where c ≠ 0 is a polynomial function of degree 0
A linear function p(x) = mx + b, where m ≠ 0 is a polynomial function of degree 1
A quadratic function p(x) = ax2 + bx + c, where a ≠ 0 is a polynomial function of degree 2
A cubic function p(x) = ax3 + bx2 + cx + a, where a ≠ 0 is a polynomial function of degree 3
A quartic function p(x) = ax4 + bx3 + cx2 + dx + e, where a ≠ 0 is a polynomial function of degree 4
A quintic function p(x) = ax5 + bx4 + cx3 + dx2 + ex + f, where a ≠ 0 is a polynomial function of degree 5
How to name a polynomial function
p(x) = 6x4 + 5x is a quartic binomial
p(x) = -2x5 + 6x4 + 9 is a quintic trinomial
p(x) = -2x5 + 6x4 + 10x3 + -3x2 + 5x + 9 is a quintic polynomial of 5 terms
p(x) = 5x + 9 is a linear binomial
p(x) = -3x2 is a quadratic monomial
p(x) = -10x3 + -3x2 + 5x + 9 is a cubic polynomial of 4 terms
Graphs of polynomial functions
The graph of a polynomial function of degree 2 or higher is smooth and continuous. The graph is smooth because it has only rounded curves with no sharp corners. The graph is continuous because it has no breaks ans can be drawn without lifting your pencil.
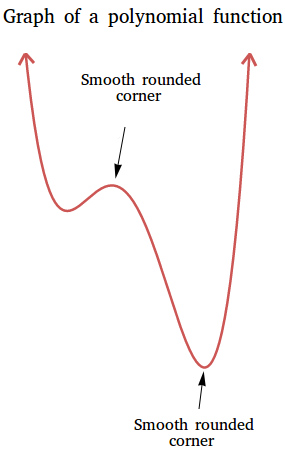
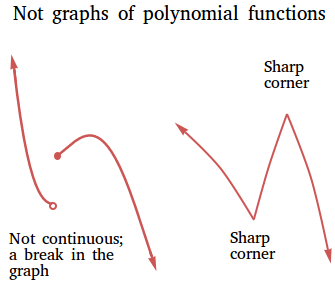
If the degree of the polynomial is 0 or 1, the graph is a straight line.
Turning points of polynomial functions
A turning point of a polynomial function is a point where the graph changes direction from increasing to decreasing or vice versa.
If f is a polynomial function of degree n, then the graph of f has at most n - 1 turning points.
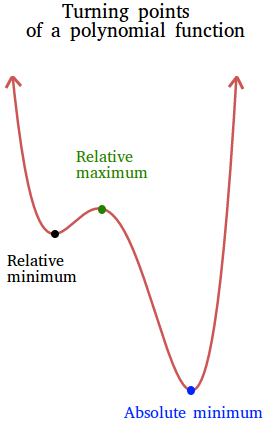
The graph in the figure immediately above has three turning points shown with a black dot, a green dot, and a blue dot. Therefore, this is the graph of a quartic polynomial function or a polynomial of degree 4.
Turning points can be maxima and/or minima.
A global minimum, also called absolute minimum, is a point on the graph where the function has its smallest value. The point shown in blue is a global minimum. You cannot find another point on the graph that is smaller than this one!
A global maximum, also called absolute maximum, is a point on the graph where the function has its greatest value. The graph above does not have a global maximum since it keeps on increasing without bound.
A local minimum, also called relative minimum, is a point on the graph where the function has the smallest value on a certain interval. The point shown in black is a relative minimum. It is a minimum on a certain portion of the graph, not when considering the whole graph!
A local maximum, also called relative maximum, is a point on the graph where the function has the greatest value on a certain interval. The point shown in green is a relative maximum. It is a maximum on a certain portion of the graph, not when considering the whole graph!
End behavior of a polynomial function
The end behavior is the behavior of a graph of a function to the far left or to the far right. Although a polynomial function will increase or decrease in some intervals, the polynomial will eventually rise or fall without bound.
The leading coefficient test is used to determine whether the graph goes up or down at each end. As the name suggests, the test depends on the leading term anxn
In particular, the test depends on the sign of the leading coefficient and the degree n of the polynomial function.
The leading coefficient test
Suppose p(x) = anxn + an-1xn-1 + ... + a2x2 + a1x1 + a0 (an ≠ 0)
If the leading coefficient is positive and the degree of n is an odd number, then p(x) falls to the left and rises to the right.
If the leading coefficient is negative and the degree of n is an odd number, then p(x) rises to the left and falls to the right.
If the leading coefficient is positive and the degree of n is an even number, then p(x) rises to the left and rises to the right.
If the leading coefficient is negative and the degree of n is an even number, then p(x) falls to the left and falls to the right.
For example, using the leading coefficient test, determine the end behavior of the parabola of f(x) = 4x2 + x - 4
Solution
First, identify the degree of the polynomial and the sign of the leading coefficient.
The degree of the polynomial is 2 and it is even.
The leading coefficient is 4 and it is positive.
Therefore, the graph rises to the left and rises to the right.