Prove that the diagonals of a rectangle are congruent
In order to prove that the diagonals of a rectangle are congruent, consider the rectangle shown below. In this lesson, we will show you two different ways you can do the same proof using the same rectangle.
The first way to prove that the diagonals of a rectangle are congruent is to show that triangle ABC is congruent to triangle DCB
Here is what is given: Rectangle ABCD
Here is what you need to prove: segment AC ≅ segment BD
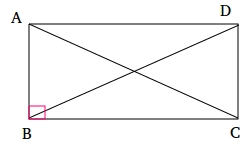
Since ABCD is a rectangle, it is also a parallelogram.
BC ≅ BC by the Reflexive Property of Congruence.
Furthermore, ∠ABC and ∠DCB are right angles by the definition of rectangle.
∠ABC ≅ ∠DCB since all right angles are congruent.
Summary
segment AB ≅ segment DC
∠ABC ≅ ∠DCB
BC ≅ BC
Therefore, by SAS, triangle ABC ≅ triangle DCB.
Since triangle ABC ≅ triangle DCB, segment AC ≅ segment BD
Things that you need to keep in mind when you prove that the diagonals of a rectangle are congruent.
Here are some important things that you should be aware of about the proof above.
- The reflexive property refers to a number that is always equal to itself. For example, x = x or -6 = -6 are examples of the reflexive property.
- SAS stands for "side, angle, side". You should perhaps review the lesson about congruent triangles.
- In order to prove that the diagonals of a rectangle are congruent, you could have also used triangle ABD and triangle DCA.
The second way to prove that the diagonals of a rectangle are congruent is to show that triangle ABD is congruent to triangle DCA
Here is what is given: Rectangle ABCD
Here is what you need to prove: segment AC ≅ segment BD
Since ABCD is a rectangle, it is also a parallelogram.
AD ≅ AD by the Reflexive Property of Congruence.
Furthermore, ∠BAD and ∠CDA are right angles by the definition of rectangle.
∠BAD ≅ ∠CDA since all right angles are congruent.
Summary
segment AB ≅ segment DC
∠BAD ≅ ∠CDA
AD ≅ AD
Therefore, by SAS, triangle ABD ≅ triangle DCA.
Since triangle ABD ≅ triangle DCB, segment AC ≅ segment BD