Prove that opposite sides of a parallelogram are congruent

Here is how we can prove that opposite sides of a parallelogram are congruent or equal using the parallelogram below.

Opposite sides of a parallelogram are congruent
Here is what is given: parallelogram ABCD

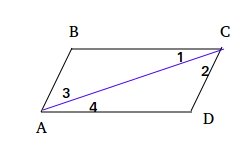
Here is what we need to prove: segment AB ≅ segment CD and segment BC ≅ AD

Since ABCD is a parallelogram, segment BC is parallel to segment AD according to the definition of a parallelogram.

By the same token, segment AB is parallel to segment DC according to the definition of a parallelogram.

Line AC is a transversal for segment BC and segment AD. This transversal creates alternate interior angles 1 and 4 which are equal as shown below.

Alternate interior angles

By the same token, Line AC is a transversal for segment AB and segment DC. This transversal creates alternate interior angles 2 and 3 which are equal.

Alternate interior angles
Moreover, segment AC ≅ segment AC by reflexive property.

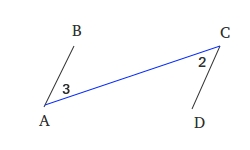
Summary

∠1 ≅ ∠ 4

∠2 ≅ ∠ 3

segment AC ≅ segment AC

By ASA, triangle ABC ≅ triangle ADC

Therefore,segment AB ≅ segment CD and segment BC ≅ AD because corresponding parts of congruent triangles are also congruent.

Things that you need to keep in mind when you prove that opposite sides of a parallelogram are congruent.

Here are some important things that you should be aware of about the proof above. 

  • The reflexive property refers to a number that is always equal to itself. For example, z = z or 1000 = 1000 are examples of the reflexive property. 
  • ASA stands for "angle, side, angle". You should perhaps review the lesson about congruent triangles if you find it hard to understand the proof.
  • A transversal is a line that cuts two or more lines
  • Notice that in the proof we were able to find two angles that have the same measure in both triangles. This means that all three angles in both triangles have the same measure. However, this information is not enough to say that the triangles are congruent.
  • The ASA postulate is most likely the only thing we can use to prove that the opposite sides of a parallelogram are congruent. 
  • If you do not know what alternate interior angles are, please review this lesson.

It is not always easy to understand proofs in geometry. Any questions about this proof, feel free to contact me.

How to prove that the diagonals of a rectangle are congruent