Unlimited Pythagorean Theorem Worksheet
The Pythagorean theorem worksheet generator below will help you generate unlimited problems with answers. You could use this generator for more practice now or after you have use the worksheet further down to introduce students to the Pythagorean theorem.
Teachers can use the worksheet below as part of a lesson plan in the classroom so that they can introduce students to the Pythagorean theorem. Scroll down to print the worksheet. Then, use the Pythagorean theorem worksheet generator above to generate more worksheets.
Name: ____________________
Date: _____________________
1. Use the figure below about the Pythagorean theorem to answer the following questions.
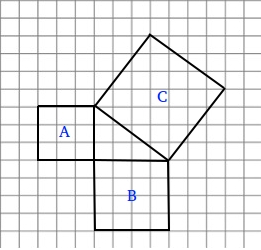
a. What is the area of square A ? __________
b. What is the area of square B ? __________
2.
a. What is the area of the triangle ? __________
b. How many of the triangle can fit in square C ? ___________
c. What is the area of the square C ? _________
3 . What is the relationship among the areas of the squares? (Hint: write an equation) _________
4. Using the equation you found in 3., write a formula for the Pythagorean theorem. __________
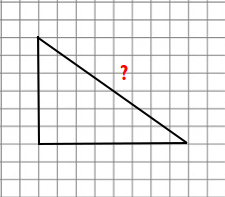
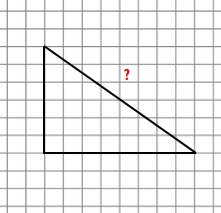
5. Find the missing length of the figure below
6. Find the missing length of the figure below
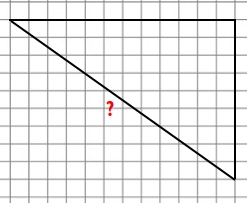
7. Find the missing length of the figure below
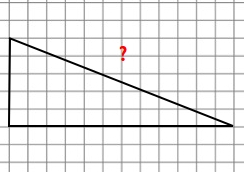
8. Find the missing length of the figure below if 2 squares represent 1 unit.
Here is what the Pythagorean theorem worksheet will help students do.
1. Looking at the areas of the squares on each of the sides of the triangles shown on the graph paper.
2. Analyze the areas found for the three squares in order to write the relationship between the area of square C and the areas of square A and square B.
3. Use the relationship between the areas of the squares to write down the Pythagorean theorem.
Moreover, students will use the Pythagorean theorem worksheet to do find the length of c or the hypotenuse when a and b are known.
This worksheet will help students draw the following conclusion:
In a right angle triangle, the square of the hypotenuse is equal to the sum of the square of the other sides of the triangle.
An example showing how to use the Pythagorean theorem
Use the Pythagorean theorem and the figure below to find the length of the hypotenuse or c.
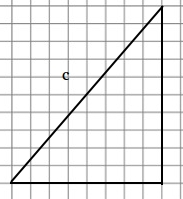
c2 = a2 + b2
1. Find a and b by counting the units. We see that a = 10 and b = 8
2. Substitute 10 and 8 in the formula
c2 = 102 + 82
Find the sum of the squares
c2 = 100 + 64
c2 = 164
Take the square root of the sum.
c = square root of 164 = 12.80
The length of the hypotenuse is 12.80.