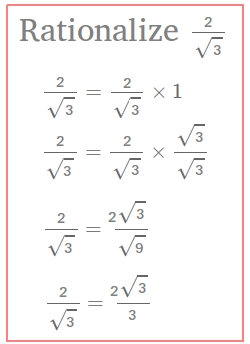Rationalizing the denominator of any radical expression
Rationalizing the denominator of a radical expression is the process of removing the radical sign in the denominator of the radical expression.
The reason perhaps mathematicians do this is because they do not like to see square root sign in the denominator.
Examples about rationalizing the denominator of a rational expression
Study the example in the image below carefully before reading the other examples in this lesson.
Example #1:
|
$$
Rationalize \ \frac{3} {\sqrt{5}} $$
|
|
Multiply both sides of the expression above by the numerical expression below.
|
$$
\frac{\sqrt{5}} {\sqrt{5}} $$
|
|
The reason we multiplied the denominator by square root of 5 is because we want to make the denominator a perfect square.
|
$$
Notice \ also \ that \ \frac{\sqrt{5}} {\sqrt{5}} = 1 $$
|
|
Therefore, it is like multiplying the expression by 1 which does not change the problem.
|
$$
\frac{3} {\sqrt{5}} = \frac{3} {\sqrt{5}} × 1 $$
|
|
|
$$
\frac{3} {\sqrt{5}} = \frac{3} {\sqrt{5}} × \frac{\sqrt{5}} {\sqrt{5}} $$
|
|
|
$$
\frac{3} {\sqrt{5}} = \frac{3 \sqrt{5}} {\sqrt{25}} $$
|
|
|
$$
\frac{3} {\sqrt{5}} = \frac{3 \sqrt{5}} {5} $$
|
|
Example #2
|
$$
Rationalize \ \frac{ \sqrt{2}} {\sqrt{8n}} $$
|
|
Multiply both sides of the expression above by the numerical expression below.
|
$$
\frac{\sqrt{2n}} {\sqrt{2n}} $$
|
|
Notice that if you had multiplied by square root of 8n, it will still be correct. Multiplying by square root of 2n will give you smaller number to deal with though and that is better.
|
$$
\frac{\sqrt{2}} {\sqrt{8n}} = \frac{\sqrt{2}} {\sqrt{8n}} × \frac{\sqrt{2n}} {\sqrt{2n}} $$
|
|
|
$$
\frac{\sqrt{2}} {\sqrt{8n}} = \frac{\sqrt{2 × 2} × \sqrt{n}} {\sqrt{8n × 2n}}$$
|
|
|
$$
\frac{\sqrt{2}} {\sqrt{8n}} = \frac{\sqrt{4} × \sqrt{n}} {\sqrt{16n^2}}$$
|
|
|
$$
\frac{\sqrt{2}} {\sqrt{8n}} = \frac{2 × \sqrt{n}} {4n}$$
|
|
|
$$
\frac{\sqrt{2}} {\sqrt{8n}} = \frac{\sqrt{n}} {2n}$$
|
|
Rationalizing the denominator of a rational expression using conjugates.
|
$$
Rationalize \ \frac{6} {\sqrt{5} - \sqrt{2}} $$
|
|
Multiply both sides of the expression above by the numerical expression below.
|
$$
\frac{\sqrt{5} + \sqrt{2}} {\sqrt{5} + \sqrt{2}} $$
|
|
|
$$
\frac{6} {\sqrt{5} - \sqrt{2}} =
\frac{6} {\sqrt{5} - \sqrt{2}} ×
\frac{\sqrt{5} + \sqrt{2}} {\sqrt{5} + \sqrt{2}} $$
|
|
|
$$
\frac{6} {\sqrt{5} - \sqrt{2}} =
\frac{6 × (\sqrt{5} + \sqrt{2}) } { (\sqrt{5} - \sqrt{2})(\sqrt{5} + \sqrt{2})} $$
|
|
|
$$
\frac{6} {\sqrt{5} - \sqrt{2}} =
\frac{6 × (\sqrt{5} + \sqrt{2}) } { (\sqrt{5})^2 - (\sqrt{2})^2} $$
|
|
|
$$
\frac{6} {\sqrt{5} - \sqrt{2}} =
\frac{6 × (\sqrt{5} + \sqrt{2}) } { 5 - 2} $$
|
|
|
$$
\frac{6} {\sqrt{5} - \sqrt{2}} =
\frac{6 × (\sqrt{5} + \sqrt{2}) } { 2} $$
|
|
|
$$
\frac{6} {\sqrt{5} - \sqrt{2}} =
3 × (\sqrt{5} + \sqrt{2}) $$
|
|