How to solve radical equations
This lesson will show how to solve radical equations. If an equation has a variable in the radicand or a variable with a fractional exponent, we call the equation a radical equation.
If the index of the radical is 2, the equation is called square root equation.
Examples of radical equations
5 + √x = 14 and x2/3 = 4 are examples of radical equations.
However, x + √5 = 2 is not a radical equation.
Solving square root equations
To solve square root equations, isolate the radical on one side of the equation. Then, raise both sides of the equation to the same power. First, study the easy example in the figure below.
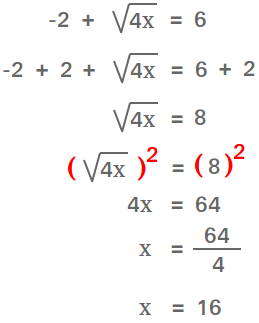
Key ideas or tricks that you will need to use to solve equations
$$ If \ \sqrt[n]{y} = c, then \ (\sqrt[n]{y})^n = c^n \ and \ y = c^n $$ $$ y^{\frac{m}{n}} = \sqrt[n]{y^m} $$More examples showing how to solve radical equations
Example #1
5 + √x = 14
Subtract 5 from each side of the equation
5 - 5 + √x = 14 - 5
√x = 9
Since we do not see any number on the top left of the radical sign, the index is 2. Since n is equal to 2, raise both sides to the power of two.
(√x)2 = 92
x = 81
5 + √x = 14 is of course a very simple radical equation to solve. Things can get a little complicated as the next example shows. In some cases, the solution of a radical equation results in two answers.
Example #2
x2/3 = 4
Using the key idea or trick above, we know we can rewrite the left-hand side of the equation as shown below. The right-hand side is still 4.
| $$ x^{\frac{2}{3}} = \sqrt[3]{x^2} $$ |
| $$ \sqrt[3]{x^2} = 4 $$ |
Since n is equal to 3, raise both sides to the power of three.
| $$ (\sqrt[3]{x^2})^{3} = 4^{3} $$ |
x2 = 64
x equal (plus or minus) square root of 64
x = 8 and x = -8
8 is the positive square root, also called principal square root.
-8 is the negative square root.
Example #3
| $$ 4 + \sqrt{3x-2} = 6 $$ |
Isolate the radical on one side of the equation. Just subtract 4 from the left side of the equation and also from the right side.
| $$ 4 - 4 + \sqrt{3x-2} = 6 - 4 $$ |
| $$ \sqrt{3x-2} = 2 $$ |
Since you are dealing with a square root equation, raise both sides of the equation to the second power. This will help you get rid of the square root symbol as shown below.
| $$ (\sqrt{3x-2})^2 = 2^2 $$ |
3x - 2 = 4
3x - 2 + 2 = 4 + 2
3x = 6
x = 2
Now, plug in 2 into the original equation to make sure that you have the right answer.
4 + √(3x - 2) = 6
4 + √(3×2 - 2) = 6
4 + √(6 - 2) = 6
4 + √4 = 6
4 + 2 = 6
6 = 6
Therefore, the only solution is x = 2
How to solve radical equations with rational exponents.
To solve equations with two radical expressions, isolate one of the radicals.
Example #4
Solve (2x + 3)0.5 - (11x + 12)0.25 = 0Isolate one radical
(2x + 3)0.5 = (11x + 12)0.25
Raise both sides of the equation to the 4th power. Notice that the reason that we raised both sides of the equation to the fourth power is because this will either get rid of the exponent or turn it into a whole number.
[(2x + 3)0.5]4 = [(11x + 12)0.25]4
(2x + 3)2 = 11x + 12
4x2 + 12x + 9 = 11x + 12
Subtract 12 from both sides of the equation.
4x2 + 12x + 9 - 12 = 11x + 12 - 12
4x2 + 12x + -3 = 11x
Subtract 11x from both sides of the equation.
4x2 + 12x - 11x + -3 = 11x - 11x
You end up with a quadratic equation of the form ax2 + bx + c = 0
4x2 + x - 3 = 0
(4x - 3)(x + 1) = 0
4x - 3 = 0
x = 3/4
x + 1 = 0
x = -1
If you would like to know how to factor the equation 4x2 + x - 3 to get (4x - 3)(x + 1), check the lesson factoring by grouping or factoring using the box method.
The alternative is to use the quadratic formula to solve the quadratic equation 4x2 + x - 3 = 0 when the equation is already in standard form. In this case, there is no need to factor.
Now, plug in -1 and 3/4 into the original equation to make sure that you have the right answer.
Here is how to show that x = -1 is a solution.
10.5 - 10.25 = 1 - 1 = 0
Here is how to show x = 3/4 is also a solution.
(6/4 + 3)0.5 - (33/4 + 12)0.25
(4.5)0.5 - (20.25)0.25
Is (4.5)0.5 - (20.25)0.25 = 0
Or is (4.5)0.5 = (20.25)0.25
Raise both sides to the 4th power
[(4.5)0.5]4 = [(20.25)0.25]4
(4.5)2 = 20.25