Revenue Function

All you need to find the revenue function is a strong knowledge of how to find the slope intercept form when a real life situation is given.

Then, you will need to use the formula for the revenue (R = x × p)

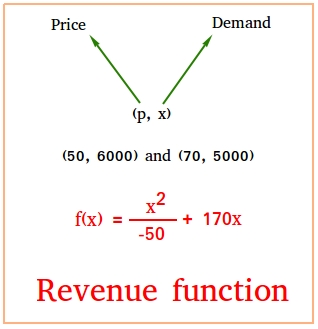
x is the number of items sold and p is the price of one item.

Real life example of the revenue function

After some research, a company found out that if the price of a product is 50 dollars, the demand is 6000. However, if the price is 70 dollars, the demand is 5000.

Find the revenue function. Then calculate f(4249), f(4250), and f(4251). What is your observation?

Solution or modeling the revenue function

Notice that the demand depends on the price of the product. The higher the price, the less the demand.

If x is the demand or how many items are sold and p is the price, we can then say that x depends on p.

As a point, you can write (p, x)

Notice that the dependent variable is always put on the right in the ordered pair.

There are two ordered pairs for the situation above. These are (50, 6000) and (70, 5000)




m = -50

x = -50p + b

To find b, use (70, 5000)

Here p = 70 and x = 5000

5000 = -50 × 70 + b

5000 = -3500 + b

5000 + 3500 = -3500 + 3500 + b

8500 = b

x = -50p + 8500

x = -50p + 8500 is the demand equation and it depends on the price.

To find the revenue function, use R = x × p


To find p, use x = -50p + 8500 to solve for p

x = -50p + 8500

x - 8500 = -50p + 8500 - 8500

x - 8500 = -50p

Divide both sides by -50



R = x × p




Instead of using R, you can use f(x) to denote that it is a function




f(4249) = -361080.02 + 722330 = 361249.98




f(4250) = -361250 + 722500 = 361250




f(4251) = -361420.02 + 722670 = 361249.98

Notice that increasing the amount of items sold from 4250 to 4251 did not increase the revenue.

This means that the maximum money you can make with this revenue function is 361250 and you are better off selling 4250 items to maximize your revenue.