Similar shapes
Similar shapes have different sizes, but the same shape. Congruent shapes have the same size and the same shape.
Circles whose radii are not the same are similar. In fact, all circles are similar because all circles must have the same shape.
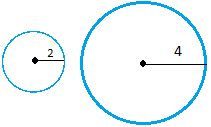
For the circles below, the ratio of the diameter of the small circle to the diameter of the big circle is
2
4
It is also perfectly OK to say that the ratio of similarity is
2
4
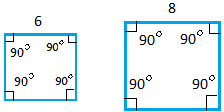
If you are comparing the smaller circle to the bigger circle, the ratio of similarity for the squares above is
|
6
8
|
or
3
4
|
Equilateral triangles are similar. Notice that just like squares all corresponding angles in an equilateral triangles are equal.
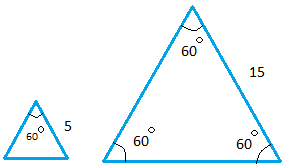
If you are comparing the smaller triangle to the bigger triangle, the ratio of similarity for the equilateral triangle is
|
5
15
|
or
1
3
|
More on corresponding angles of similar shapes.
We said before that all corresponding angles of similar figures are equal. In other words, if a figure is similar, the corresponding angles are equal.However, if the corresponding angles are equal, the figures may not be similar since they may have different shapes as shown below in that specific case.
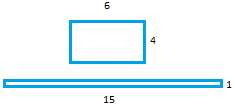
Moreover, when shapes are disproportionate or not similar, it is not possible to get the same ratio of similarity.
A ratio of the rectangle on top to the rectangle at the bottom gives different answers.
6
15
4
1
The two ratios above are clearly not equal.
It is quite possible though to create similar rectangles with the same shape.
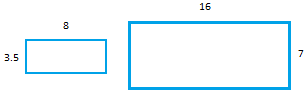
And of course the ratios above have equal values.
|
16
8
|
=
7
3.5
= 2
|
Shapes or figures don't have to look familiar or look like math shapes you are already accustomed to in order to be similar.
All shapes below are similar although some of them look kind of weird (The last one looks like an alien ).
The most important thing to keep in mind is that they all have the exact same shape although they are not the same size.

Please review the lesson about ratio if you are having a hard time understanding this lesson about similar shapes.