Similar triangles

Similar triangles are triangles whose corresponding angles are equal. This does not mean that corresponding sides are also equal. If the sides are also equal, we say that the triangles are congruent.

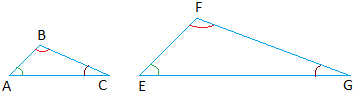
Triangle ABC and triangle EFG are similar for the following reasons:

The corresponding angles are equal.

• Angle A and angle E shown in green are equal.

• Angle B and angle F shown in red are equal.

• Angle C and angle G shown in dark red are equal.

You don't have to have the measure of all 3 corresponding angles to conclude that triangles are similar.

Angle angle similarity postulate or AA similarity postulate and similar triangles

If two angles of a triangle have the same measures as two angles of another triangle, then the triangles are similar. Why is it so?

The angles in a triangle must add up to 180 degrees.

Consider this situation:

Triangle #1:

Angle #1 = 30 degrees. Angle #2 = 80 degrees

Triangle #2:

Angle #1 = 80 degrees. Angle #2 = 30 degrees

The last angle must be the same

Triangle #1: last angle = 180 - 30 - 80 = 70

Triangle #2: last angle = 180 - 80 - 30 = 70

All 3 angles are the same, so the triangles are similar.


Look at the triangles below. According to the AA similarity postulate, they are similar.



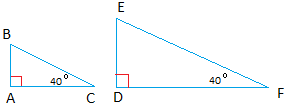
We know they are similar because angle A = angle D and angle C = angle F.

We don't really care about the measure of the last angle.

We can put the small triangle on the left inside the triangle on the right.


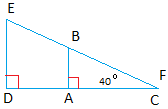
The triangles are still similar. The only difference this time is that angle C coincides with angle F.

A special figure that always gives similar triangles

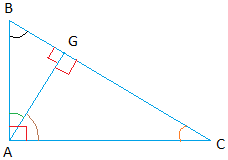
There are 3 triangles in the figure above

Triangle ABC, ABG, and AGC. All 3 triangles are similar to one another.

The easiest way to see why they are similar triangles is to plug in some numbers.

Let's say that angle B = 50°

Some important calculations:

In triangle ABG, the angle in green = 40° since 40° + 50° + 90° = 180°

The angle in brown in triangle AGC = 50° since 40° + 50° = 90°

Angle C = 40° since 50° + 40° + 90° = 180°

The result is summarized in the figure below:





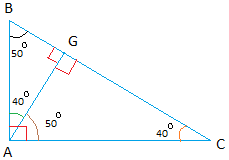
Remember all we need to prove similarity is to find 2 corresponding angles that are equal.

Show triangle ABC is similar to triangle ABG

For triangle ABC, angle A = 90° and angle B = 50°

For triangle ABG, angle G = 90° and angle B = 50°

Triangle ABC is similar to triangle ABG

Show triangle ABC is similar to triangle AGC

For triangle ABC, angle A = 90° and angle B = 50°

For triangle AGC, angle G = 90 ° and angle in brown = 50°

Triangle ABC is similar to triangle AGC

Show triangle ABG is similar to triangle AGC

For triangle ABG, angle B = 50° and angle in green = 40°

For triangle AGC, angle in brown = 50 ° and angle C = 40°

Triangle ABG is similar to triangle AGC