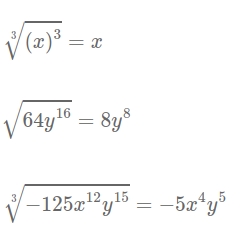Simplifying radicals containing variables

Special care must be taken when simplifying radicals containing variables. We will start with perhaps the simplest of all examples and then gradually move on to more complicated examples .

$$ \sqrt{x^2} = ??? $$

Let us look at a few examples in this form. If x = 3 or x = 5, then we have

$$ \sqrt{3^2} = \sqrt{9} = 3 = x $$
$$ \sqrt{5^2} = \sqrt{25} = 5 = x $$
These examples show that

$$ \sqrt{x^2} = x $$

Now, let us look at an example where x is a negative number. Let x  = -6

$$ \sqrt{(-6)^2} = \sqrt{36} = 6 $$

When x is negative, the answer is not just x or -6 as we saw before. The answer is positive. To make sure that the answer is always positive, we need to take the absolute value.  

$$ For\ any \ number \ y,\ \sqrt{y^2} = |y| $$

Now what about the cube root of x? The cube root of x will behave a little differently. 

$$ \sqrt[3]{x^3} = ??? $$


If x  = 2 or x = -2, the answer is not always positive.

$$ \sqrt[3]{2^3} = \sqrt[3]{8} = 2 = x $$
$$ \sqrt[3]{(-2)^3} = \sqrt[3]{-8} = -2 = x $$

As you can see here, the answer is always x

$$ For\ any \ number \ x,\ \sqrt[3]{(x)^3} = x $$

Interesting or challenging examples of simplifying radicals containing variables

Example #1:

Simplify the following radical expression.

$$ \sqrt{64y^{16}} $$


The trick is  to  write  the  expression  inside  the  radical as 

$$ \sqrt{(something)^{2}} $$

Then, 

$$ \sqrt{(something)^{2}} = something $$

We will need to use some properties of exponents to do this. 

$$ \sqrt{64y^{16}} = \sqrt{8^2 \times (y^{8})^2} = \sqrt{[8y^{8}]^2}$$

Notice that something is equal to 8y8

$$ Therefore, \sqrt{64y^{16}} = 8y^8 $$

Let us now conclude this lesson with the last example below

$$ \sqrt[3]{-125x^{12}y^{15}} $$

 Try  to  write  the  expression  inside  the  radical as 

$$ \sqrt[3]{(something)^{3}} $$

Then,

$$ \sqrt[3]{(something)^{3}} = something $$


$$ \sqrt[3]{-125x^{12}y^{15}} = \sqrt[3]{(-5)^3(x^4)^3(y^5)^3} $$


$$ \sqrt[3]{-125x^{12}y^{15}} = \sqrt[3]{[(-5)(x^4)(y^5)]^3} $$


Therefore, 

$$ \sqrt[3]{-125x^{12}y^{15}} = -5x^4y^5 $$

Take a look at the following radical expressions. We already solved them above. Do you understand how we got the answer? If so, way to go!

Simplifying radicals containing variables

Adding and subtracting radicals

Simplifying radical expressions worksheet



Tough algebra word problems

100 Tough Algebra Word Problems.

If you can solve these problems with no help, you must be a genius!

Math quizzes

 Recommended