Slope calculator

Given two points, this slope calculator will compute the slope and show step-by-step how to find the slope-intercept form and point-slope form of the line.

Guidelines to follow when using the slope calculator

Use this calculator only to check your answers. You are responsible to know how to compute the slope and get the slope-intercept form of the line.

Given two points  (5, 2) and (1, 1), you can enter (5, 2) in the boxes labeled "(x₁, y₁)" or the boxes labeled "(x₂, y₂)". You will still get the same answer.

If you type (5,2) in the boxes labeled "(x₂, y₂)" and (1,1) in the boxes labeled "(x₁, y₁)", the calculator will show 0.25 in the box labeled "Slope = m ="

Types of slope 

The slope of a line can be positive, negative, zero, or undefined.

If x₁ = x₂, the calculator will display "undefined slope"

If y₁ = y₂, the calculator will display "0"

With a negative slope, you will need see a negative sign "-" while a positive slope will display no sign. 

If you do not know how to find the slope or you need to remind yourself how to find the slope, check this lesson to get a thorough review.

Brief review on how to find the slope and the slope-intercept form without a slope calculator.

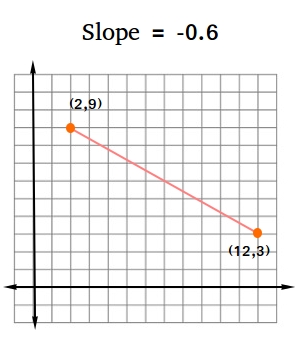
If you want to find the slope using the two points (2,9) and (12,3), you can use the following formula:

Let (x₁, y₁) = (12,3) and (x₂, y₂) = (2,9)

The slope calculator will also show that the slope-intercept form is y =  -0.6x + 10.2

Here is how to find the slope-intercept form.

The slope-intercept form is y = mx + b

So, y = -0.6x + b. 

Substitute either (2,9) or (12,3) for (x,y) in y = -0.6x + b

Using (2,9), 9 = -0.6(2) + b

9 = -1.2 + b

b = 9 + 1.2 = 10.2

y = -0.6x + 10.2

Now, enter (2,9) and (12,3) in the slope calculator above and you will see that you will get the same answer.