Slope Intercept Form

Linear Equation Builder - Slope-Intercept Form

Learn how to write equations in slope-intercept form: y = mx + b

The slope intercept form of a linear equation is y = mx + b, where m is the slope and b is the y-intercept. The graph of a linear equation is a line and y = mx + b is one of the most common forms to write the equation of a line.

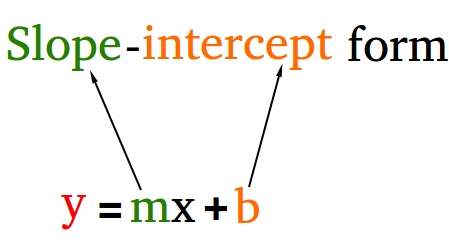
How to Derive the Slope Intercept Form of a Linear Equation

Consider an arbitrary point (x,y) on the line and a point (0,b) on the y-axis. Then, you can use the slope formula to derive the slope-intercept form. 

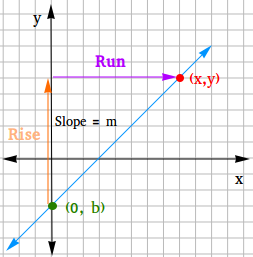
Slope = Rise / Run = (y₁ - y₂) / (x₁ - x₂)

Using (x₁,y₁) = (x,y) and (x₂,y₂) = (0,b), compute the slope m.

m = (y - b) / (x - 0)

m = (y - b) / x

Multiply both sides of the equation by x

(x)m = y - b

mx = y - b

Add b to both sides of the equation

mx + b = y - b + b

y = mx + b

Slope Intercept Formula

Examples Showing how to Find the Slope-Intercept Form of a Straight Line

The goal of these exercises is to write the equation of a straight line in slope-intercept form (y = mx  + b) by considering the following cases:

• The slope and the y-intercept are given (example #1)

• The slope and a point on the line are given (example #2)

• Two points on the line are given (example #3)

Example #1

If the slope of a line is m = 2 and the y-intercept is b = 5, write the slope intercept form of the line.

The equation is y = 2x + 5.

Example #2

If the slope of a line is m = 5 and (1, 6) is a point on the line, find the slope intercept form of the line.

This time we have m, but b is missing, so we have to find b.

Since m = 5, y = mx + b becomes y = 5x + b.

Now, use (1, 6) to get b.

Since x = 1 and y = 6, you can replace them into the equation.

Substituting 1 for x and 6 for y gives 6 = 5×1 + b.

6 = 5×1 + b is just a linear equation that you can solve to get b.

6 = 5×1 + b

6 = 5 + b

Subtract 5 from both sides.

6 − 5 = 5 − 5 + b

1 = 0 + b

1 = b

Now since we have b, y = 5x + 1

Example #3

Suppose (2, 3) and (4, 9) are two points on a line. Find the slope intercept form of the line.

This time both m and b are missing, so the first thing to do is to get m and then use m and a point, either (2, 3) or (4, 9) to get b.

Let x₁ = 4, y₁ = 9 and x₂ = 2, y₂ = 3

m = (y₁ − y₂) / (x₁ − x₂) = (9 − 3) / (4 − 2 ) = 6 / 2 = 3

Now we can use the value for m and one point to get b as already done in example #2.

Although you have two points, It does not matter which point you choose. Since both points are on the line, they will yield similar results.

Choosing (2, 3), x = 2 and y = 3

Substituting 2 for x, 3 for y, and 3 for m into the equation y = mx + b we get:

3 = 3 × 2 + b

3 = 6 + b

Subtract 6 from both sides

3 − 6 = 6 − 6 + b

-3 = 0 + b

-3 = b

Now we have b = -3 and m = 3, y = 3x + -3

Slope Intercept Form Special Cases

The y-intercept b is equal to zero

In this case, y = mx and the line always goes through the origin of the coordinate system.

The slope of the line is equal to zero

In this case, y = (0)x + b = b and when you graph the line, it will be a horizontal line as it crosses the y-intercept.

The slope of the line is undefined

In this case, x is equal to the x-coordinate of any point on the line or any other number that is given to you in an exercise. When you graph the line, it will be a vertical line as it crosses the x-intercept.