Slugging percentage
The slugging percentage (SLG) may be used to determine which player is better when two or more players have the same or almost the same batting average.
This percentage is calculated by using the formula below.
Some useful terminology
Total bases = Number of bases covered
Number of official at bats = Any turn as a batter
Home run = 4 bases
Triple = 3 bases
Double = 2 bases
Single = 1 base
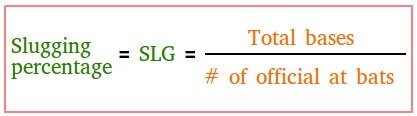
The higher the slugging percentage, the better the player.
When the percentage is high, it means that the player has hit the ball farther or better resulting in getting to more bases or home runs.
However, a factor that will influence the SLG is the number of outs.
The more outs, the lower the SLG.
So, a player can maximize the SLG by increasing the number of bases and decreasing the number of outs.
When computing this SLG, we usually round decimal answers to three places.
A few real-life examples that will show you how to find the slugging percentage
Example #1:
During a baseball game, a player had the following performance:
3 home runs
5 triples
12 doubles
20 singles
40 outs
What is the player's slugging percentage?
3 home runs = 3 × 4 = 12 bases.
5 triples = 5 × 3 = 15
12 doubles = 12 × 2 = 24
20 singles = 20 × 1 = 20
Total bases = 12 + 15 + 24 + 20 = 71
Total at bats is found by adding everything shown in bold above.
Total at bats = 3 + 5 + 12 + 20 + 40 = 80
SLG = (Total bases)/(Number of official at bats)
SLG = (71)/(80)
SLG = 0.8875
After rounding to three decimals place, we get 0.888
Example #2:
During a baseball game, a player had the following performance:
1 home run
6 triples
14 doubles
25 singles
30 outs
What is the player's SLG?
1 home run = 1 × 4 = 4 bases.
6 triples = 6 × 3 = 18
14 doubles = 14 × 2 = 28
25 singles = 25 × 1 = 25
Total bases = 4 + 18 + 28 + 25 = 75
Total at bats is found by adding everything shown in bold above.
Total at bats = 1 + 6 + 14 + 25 + 30 = 76
SLG = (Total bases)/(Number of official at bats)
SLG = (75)/(76)
SLG = 0.98684
After rounding to three decimals place, we get 0.987