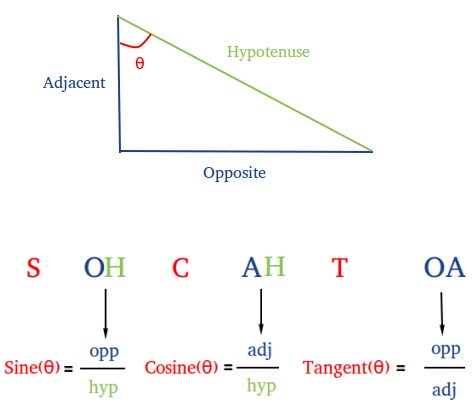
SOHCAHTOA

SOHCAHTOA (pronounced: so-cah-tow-ah) is a very useful mnemonic that can help students remember the sine ratio, cosine ratio, and the tangent ratio of the three basic trigonometric functions sine, cosine, and tangent.

SOH : Sine = Opposite / Hypotenuse 

CAH : Cosine = Adjacent / Hypotenuse 

TOA : Tangent = Opposite / Adjacent 

As you can see in the image below, the sides of a right triangle are the opposite side, the adjacent side, and the hypotenuse.

  • The opposite side of a right triangle is the side opposite the angle θ. 
  • The adjacent side of a right triangle is the side adjacent or next to the angle θ.
  • The hypotenuse of a right triangle is the longest side or the side opposite the right angle.
SOHCAHTOA

Study the nice figure shown above carefully! It will help you greatly to remember the acronym sohcahtoa, which is a memory aid that can help you the following important ratios

sin θ = opposite side / hypotenuse

cos θ = adjacent side / hypotenuse

tan θ = opposite / adjacent

You could also use the following mnemonic to remember the trigonometric ratios.

" Some Old Hog Came Around Here and Took Our Apples."

A couple of examples showing how to use sohcahtoa to evaluate trigonometric functions

Example #1

Use the triangle below to find the values of sin θ, cos θ, and tan θ

An example showing how to use sohcahtoa

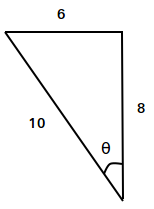
sin(θ) = opposite side / hypotenuse = 6/10 = 0.6

cos(θ) = adjacent side / hypotenuse= 8/10 = 0.8

tan(θ) = opposite / adjacent = 6/8 = 0.75

Example #2

Use the triangle below to find the values of sin θ, cos θ, tan θ, csc θ, sec θ, and cot θ

sohcahtoa

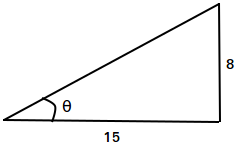
First, we need to find the length of the hypotenuse using the Pythagorean theorem.

c2 = 152 + 82

c2 = 225 + 64

c2 = 289

c = √289

c = 17

sin(θ) = opposite side / hypotenuse = 8/17 

cos(θ) = adjacent side / hypotenuse = 15/17 

tan(θ) = opposite / adjacent = 8/15

csc(θ) = hypotenuse / opposite side = 17/8 

sec(θ) = hypotenuse / adjacent side = 17/15 

cot(θ) = adjacent / opposite = 15/8

SOHCAHTOAFAQs

No, SOHCAHTOA is not a real word. It is like an abbreviation formed from the initial letters of the words (sine opposite hypotenuse),(cosine adjacent hypotenuse), and (tangent opposite adjacent).
Yes, you can only use SOHCAHTOA when solving right triangles. If the triangle is not a right triangle, you can use the law of sines and/or the law of cosines.
The S in SOH stands for sine.
You can use SOHCAHTOA to solve a right triangle. You solve a right triangle by looking for missing sides and/or missing angles.
SOHCAHTOA is not a formula. It is a way to remember the right triangle definitions or the trigonometric ratios of sine, cosine, and tangent.

Trigonometric identities