Solving Two-Step Equations
When solving two-step equations, these equations will have the following linear form: ax + b = c or ax − b = c, where a is called coefficient and b and c are called constants.
Of course, only two steps are needed as shown below:
Step 1
Isolate ax
Step 2
Isolate x
Remember also the Golden Rule of Algebra. Whatever you do to one side of an equation, you must also do the same to the other side of the equation in order to keep the equation balanced.
Solving two-step equations of the form ax - b = c

Example #1
Solve 2x - 2 = 6
Step 1:
Isolate 2x by adding 2 to both sides of 2x - 2 = 6
2x - 2 + 2 = 6 + 2
2x = 8
Step 2:
Divide both sides of 2x = 8 by 2 to isolate x
2x / 2 = 8 / 2
x = 4
You can check to see if x = 4 is indeed a solution by replacing 4 in the original equation.
2(4) - 2 = 8 - 2 = 6 ✓
Generally speaking, when solving equations of the form ax − b = c, you can add b to both sides of the equation to isolate ax (step 1) and then divide both sides by a to isolate x (step 2).
ax - b = c
Step 1:
ax - b + b = c + b
ax + 0 = c + b
ax = c + b
Step 2:
ax/a = (c + b)/a
x = (c + b)/a
Solving two-step equations of the form ax + b = c
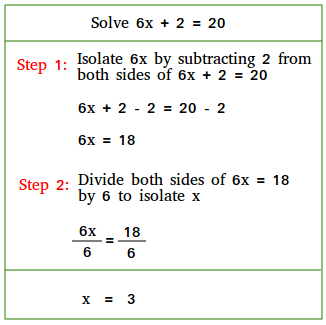
Example #2
Solve 6x + 2 = 20
Step 1:
Isolate 6x by subtracting 2 from both sides of 6x + 2 = 20
6x + 2 - 2 = 20 - 2
6x = 18
Step 2:
Divide both sides of 6x = 18 by 6 to isolate x
6x / 6 = 18 / 6
x = 3
In general, when solving equations of the form ax + b = c, you can subtract b from both sides of the equation to isolate ax (step 1) and then divide both sides by a to isolate x (step 2).
ax + b = c
Step 1:
ax + b - b = c - b
ax + 0 = c - b
ax = c - b
Step 2:
ax/a = (c - b)/a
x = (c - b)/a
There is nothing special about subtracting b or adding b to both sides and then divide by a! In practice, mathematicians prefer to add or subtract something from both sides and then divide by a because calculations are usually easier.
Notice though that there is another way to solve example #1 above with just two steps as well.
1. The first step is to divide both sides of the equation by a
2. The second step is to either add something to both sides of the new equation or subtract something from both sides of the new equation.
Solve 2x - 2 = 6 by following the two steps outlined immediately above
Step 1:
Divide both sides of 2x - 2 = 6 by 2
(2x - 2) / 2 = 6 / 2
x - 1 = 3
Step 2:
Add 1 to both sides of x - 1 = 3
x - 1 + 1 = 3 + 1
x = 4
Solving two-step equations involving fractions

Example #3
Solve (2/5)x + 4 = 14
Step 1:
Isolate (2/5)x by subtracting 4 from both sides of (2/5)x + 4 = 14
(2/5)x + 4 - 4 = 14 - 4
(2/5)x = 10
Step 2:
Multiply both sides of (2/5)x = 10 by the reciprocal of 2/5 or 5/2.
(5/2)(2/5)x = 10(5/2)
(10/10)x = 50/2
x = 25
Again, we can also solve example #3 by dividing both sides by 2/5 first.
(2/5)x + 4 = 14
Divide both sides by 2/5
[(2/5) ÷ (2/5)]x + 4 ÷ 2/5 = 14 ÷ 2/5
[1]x + 4/1 ÷ 2/5 = 14/1 ÷ 2/5
x + 4/1 × 5/2 = 14/1 × 5/2
x + 20/2 = 70/2
x + 10 = 35
Subtract 10 from both sides
x + 10 - 10 = 35 - 10
x + 0 = 25
x = 25
Solving two-step equations involving decimals
The steps to follow are the same when solving two-step equations involving decimals.
Example #4
Solve 3.1x + 1.2 = 7.4
Subtract 1.2 from both sides of 3.1x + 1.2 = 7.4 to isolate 3.1x
3.1x + 1.2 - 1.2 = 7.4 - 1.2
3.1x = 6.2
Divide both sides of 3.1x = 6.2 by 3.1 to isolate x
(3.1x)/3.1 = 6.2/3.1
x = 2
The super fast way to solve two-step equations.
When taking a test, there is no need to follow all the steps above if all you need to do is to choose the right answer from a list of multiple choices.
To solve ax + b = c, just use x = (c - b)/a
You can solve example #2 or 6x + 2 = 20 very fast.
x = (20 - 2)/6 = 18/6 = 3
Similarly, you can solve example #1 or 2x - 2 = 6 very fast.
x = (c + b)/a = (6 + 2)/2 = 8/2 = 4
Linear equations calculatorEasily solve equations of the form ax + b = c with the click of a button!