Sum of all exterior angles of a polygon
To help you see what the sum of all exterior angles of a polygon is, we will use a square and then a regular pentagon. Since it is very easy to see what the sum is for a square, we will start with the square. You can also use rectangles!
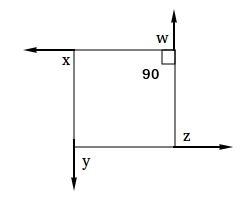
Notice that an exterior angle is formed by a side of the square and an extension of an adjacent side. For example in the figure below, angle x, angle y, angle z, and angle w are all exterior angles.
Each interior angle in a square is equal to 90 degrees. Notice that the sum of an interior angle plus the adjacent exterior angle is equal to 180 degrees.
Interior angle + adjacent exterior angle = 180 degrees.
In fact, the sum of (one interior angle plus the adjacent exterior angle) of any polygon always add up to 180 degrees. This is so because when you extend any side of a polygon, what you are really doing is extending a straight line and a straight line is always equal to 180 degrees.
For example, 90 degrees + w = 180 degrees
90 degrees - 90 degrees + w = 180 degrees - 90 degrees
0 + w = 90 degrees
w = 90 degrees
Since there are 4 exterior angles, 4 x 90 degrees = 360 degrees.
Sum of all exterior angles of a polygon: pentagon
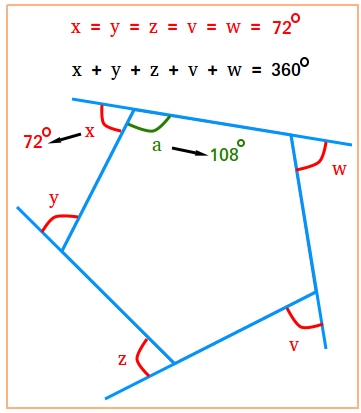
In the figure or pentagon above, we use a to represent the interior angle of the pentagon and we use x,y,z,v, and w to represents the 5 exterior angles.
To find the measure of the interior angle of a pentagon, we just need to use this formula.
The interior angle of any polygon = [(n - 2 ) 180] / n
Since n is equal to 5, [(n - 2 ) 180] / n = [(5 - 2) 180] / 5 = [3 x 180] / 5 = 540 / 5 = 108
∠x and ∠a are adjacent (common side and common vertex) and supplementary.
Again, interior angle + adjacent exterior angle = 180 degrees.
108 degrees + adjacent exterior angle = 180 degrees
108 degrees - 108 degrees + adjacent exterior angle = 180 degrees - 108 degrees
0 + adjacent exterior angle = 180 degrees - 108 degrees
Adjacent exterior angle = 72 degrees
Since there are 5 exterior angles, 5 x 72 = 360 degrees.
It does not matter how many sides the polygon has!
Exterior angle sum theorem
The sum of all exterior angles of a polygon is always equal to 360 degrees.
Another way to look at the sum of the exterior angles of a polygon
As already shown, we know that interior angle + adjacent exterior angle = 180 degrees.
interior angle + adjacent exterior angle = 180 degrees
interior angle - interior angle + adjacent exterior angle = 180 degrees - interior angle
adjacent exterior angle = 180 degrees - interior angle
Since a square has 4 exterior angles, just multiply the equation above by 4 to get the sum of its exterior angles.
Sum of all exterior angles of a square
4(adjacent exterior angle) = 4(180 degrees - interior angle)
4(adjacent exterior angle) = 4(180 degrees) - 4(interior angle)
The sum of the exterior angles = 4(adjacent exterior angle)
The sum of the exterior angles = 4(180 degrees) - 4(90 degrees)
The sum of the exterior angles = 720 degrees - 360 degrees
The sum of the exterior angles = 360 degrees
Sum of all exterior angles of a pentagon
Similarly, since a pentagon has 5 exterior angles, we get the following equation
The sum of the exterior angles = 5(180 degrees) - 5(interior angle)
The sum of the exterior angles = 5(180 degrees) - 5(108)
The sum of the exterior angles = 900 - 540
The sum of the exterior angles = 360
How to prove that the sum of exterior angles of any polygon is equal to 360 degrees?
Suppose the number of sides of a polygon is n. Show that the sum of all exterior angles of the polygon is 360 degrees.
n(adjacent exterior angle) = n(180 degrees - interior angle)
n(adjacent exterior angle) = n(180 degrees) - n(interior angle)
n(adjacent exterior angle) = sum of exterior angles of any polygon
interior angle = [(n - 2 )180] / n
The sum of exterior angles of any polygon = n(180 degrees) - (n)[(n - 2)180] / n
The sum of exterior angles of any polygon = 180n - (n - 2)180
The sum of exterior angles of any polygon = 180n - (180n - 360)
The sum of exterior angles of any polygon = 180n - 180n + 360
The sum of exterior angles of any polygon = 360
Notice that the sum of the interior angles = (n)[(n - 2)180] / n = (n - 2)180