|
 |
|||||
Surface area of a square pyramidIt is not complicated to derive the formula of the surface area of a square pyramid. start with a square pyramid as shown below and call the length of the base s and the height of one triangle l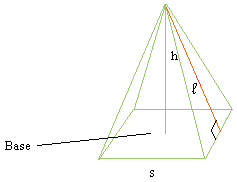  The word slant refers also to something that is oblique or bent, or something that is not vertical or straight up. Basically, anything that is not horizontal or vertical! The area of the square is s2 The area of one triangle is (s × l)/2 Since there are 4 triangles, the area is 4 × (s × l)/2 = 2 × s × l Therefore, the surface area, call it SA is: SA = s2 + 2 × s × l : Example #1: Find the surface area of a square pyramid with a base length of 5 cm, and a slant height of 10 cm SA = s2 + 2 × s × l SA = 52 + 2 × 5 × 10 SA = 25 + 100 SA = 125 cm2 Example #2: Find the surface area with a base length of 3 cm, and a slant height of 2 cm SA = s2 + 2 × s × l SA = 32 + 2 × 3 × 2 SA = 9 + 12 SA = 21 cm2 Example #3: Find the surface area with a base length of 1/2 cm, and a slant height of 1/4 cm SA = s2 + 2 × s × l SA = (1/2)2 + 2 × 1/2 × 1/4 SA = 1/4 + 1 × 1/4 SA = 1/4 + 1/4 SA = 2/4 SA = 1/2 cm2
 |
|
|||||
IntroductionArithmeticGeometryGraph it!Probability and statisticsReal life mathSequences and patternsAlgebraResourcesTeachers!
|
||||||
| Advertising on basic-mathematics.com | ||||||
|
| ||||||
