How to derive the number pi = π = 3.1415926...

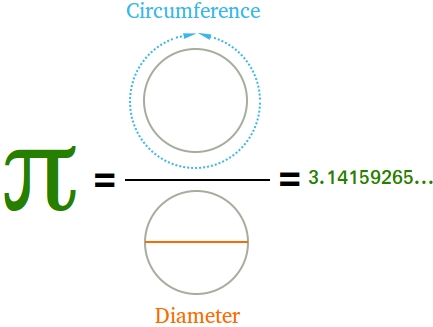
The number pi (π) is equal to 3.14159265 seven places after the decimal point.

It is commonly used when calculating the circumference and the area of a circle, which formulas are equal to 2 × π × r and π × r² respectively.

An experiment or activity you can do at home that will show you how to derive the number pi

Ever wondered where pi came from or why pi is equal to 3.1415926? You can derive the number pi by doing the following experiment:

Take any piece of string. Use a ruler to measure the length of the string in inches, centimeters or any units you want.

Write down the length of the string you just measured on a piece of paper. 

Now play with the string until you make a circle with it. Then, use a ruler to measure the diameter of the circle.

Write down the length of the diameter you just on a piece of paper as well.

Do a ratio of the circumference to the diameter. In other words, divide the length of the string by the diameter.

You should find something very close to 3.1415926.

The piece of string you see on the picture above has a length of about 22 inches and I found a diameter of 7 inches. 22 divided by 7 is equal to 3.142857143.

It is not equal exactly to 3.1415926, but it is ok because in practice we use 3.14 to do calculation.

All we needed here was a good approximation.

Repeat the experiment above with a longer or a shorter piece of string.

You should find a similar answer for pi because the size for the circle does not matter.

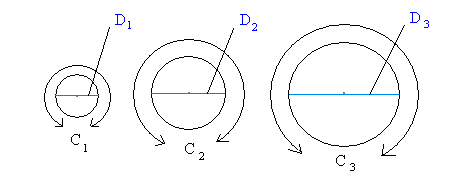
In general, regardless of the size of the circle, the following is always true.



Since D = 2 × r, the formula above can also be written as C = 2 × π × r