Area of a trapezoid calculator

This trapezoid calculator will compute the area of a trapezoid for you. Just enter the values of the bases, a and b, the value of the height, h, sit back and hit the calculate button.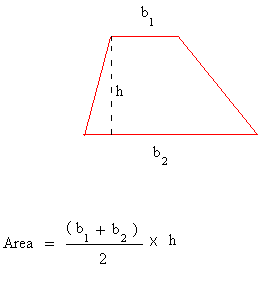


Remember that the formula to get the area of a trapezoid is:



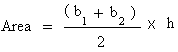
So, if b₁ = 2 cm, b₂ = 4 cm, and h = 6 cm

(b₁ + b₂)/2 = (2 + 4)/2 = 6/2 = 3

A= 3 × 6 = 18 cm²

Guidelines to follow when using the trapezoid calculator

Convert fractions into decimals before entering them, so do not enter any number with a slash "/ " 

Do not enter negative number since a distance cannot be negative.

Do not enter the unit. For example, for 15 cm, just enter 15.

Examples showing how to use the calculator in order to find the area of a trapezoid.

Example #1

Use the trapezoid calculator to find the area of a trapezoid with bases 6 cm and 9 cm and height 5 cm.

Enter 6 in the box that is labeled 'Enter the value of base b₁'

Enter 9 in the box that is labeled 'Enter the value of base b₂'

Enter 5 in the box that is labeled 'Enter the height h'

Hit the button labeled 'Calculate'

The calculator will display 37.5 in the box labeled ' The area of the trapezoid is' 

The area of the trapezoid is 37.5 cm²

Example #2

The end of a gold bar usually has the shape of a trapezoid. Use the trapezoid calculator to find the area of the end of the gold bar with bases 4 cm and 2 cm and height 3 cm.

Enter 4 in the box that is labeled 'Enter the value of base b₁'

Enter 2 in the box that is labeled 'Enter the value of base b₂'

Enter 3 in the box that is labeled 'Enter the height h'

Hit the button labeled 'Calculate'

The calculator will display 9 in the box labeled ' The area of the trapezoid is' 

The area of the end of the gold bar is 9 cm²