Trigonometric ratios of special angles

This lesson will summarize the trigonometric ratios of special angles taken from lesson #1 to lesson #6. We show you these results here before we move on to more complicated topics.

By special angles, we mean 30 degrees, 45 degrees, and 60 degrees.

These are the angles from the 45-45-90 degrees triangle and the 30-60-90 degrees triangle.

In lesson #1, we saw that tan(45 degrees) = 1

In lesson #2 and lesson #4, we saw that sin(45 degrees) = 1 / √(2) = √(2) / 2

We also saw that cos(45 degrees) = 1 / √(2) = √(2) / 2

If you are not convinced that 1 / √(2) = √(2) / 2, use a calculator to prove this to yourself.

Here is the math though showing why 1 / √2 = √2 / 2

Multiply both the numerator and the denominator of 1 / √2 by √2. 

(1 × √2) / ( √2 × √2) = (√2) / [√(2 × 2)] = (√2) / √4 = (√2) / 2

In lesson #5 and lesson #6, we got the following results:

cos(30 degrees) = y / 1 = y = √3 / 2

cos(60 degrees) = x / 1 = x = 1 / 2

sin(60 degrees) = y / 1 = y = √3 / 2

sin(30 degrees) = x / 1 = x = 1 / 2

The only trigonometric ratios we don't have are tan(30 degrees) and tan(60 degrees)

To get these, we will use the same triangle we use in lesson #5 to find the sine and cosine of 30 degrees and 60 degrees.









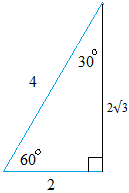
1 / √ (3) = √(3) / 3 (Just like 1 / √ (2) = √(2) / 2 )

Now, here is the table summarizing the trigonometric ratios of special angles

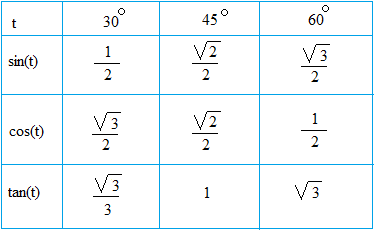
Some teachers will ask you to memorize the trigonometric ratios of these special angles. Some teachers may not. It is not a bad idea though to know it by heart or be able to reproduce it quickly. Look at the table carefully. Is there some type of pattern or mnemonic that make it easy to reproduce the trigonometric ratios of these special angles?

Notice that for sine, the denominator is always 2. For the numerators, start at 1 and count up until you reach 3. Then, just take the square root of each number. Notice that √(1) = 1.

For cosine, just write everything backward. For tangent, just do the math that is tan(x) = sin(x) / cos(x).