Volume of a cone

Given the radius or r and the height or h, the volume of a cone can be found by using the formula:

Formula: V_cone = 1/3 × b × h
b is the area of the base of the cone. Since the base is a circle, area of the base = π × r²

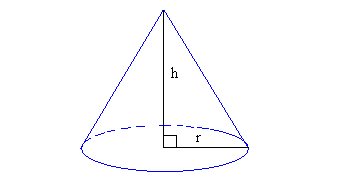
Thus, the formula to use to find the volume is V_cone = 1/3 × π × r² × h

Use π = 3.14

Some examples that will show how to find the volume of a cone.

Example #1:

Calculate the volume if r = 2 cm and h = 3 cm

V_cone = 1/3 × 3.14 × 2² × 3

V_cone = 1/3 × 3.14 × 4 × 3

V_cone = 1/3 × 3.14 × 12

V_cone = 1/3 × 37.68

V_cone = 1/3 × 37.68/1

V_cone = (1 × 37.68)/(3 × 1)

V_cone = 37.68/3

V_cone = 12.56 cm³


Example #2:

Calculate the volume if r = 4 cm and h = 2 cm

V_cone = 1/3 × 3.14 × 4² × 2

V_cone = 1/3 × 3.14 × 16 × 2

V_cone = 1/3 × 3.14 × 32

V_cone = 1/3 × 100.48

V_cone = 1/3 × 100.48/1

V_cone = (1 × 100.48)/(3 × 1)

V_cone = 100.48/3

V_cone = 33.49 cm³

An example showing how to find the volume of an oblique cone.

Since the formula to find the volume of a cone applies to all cones, including oblique cone, we can use the formula V = 1/3(π×r²×h)

Example #3:

Find the volume of an oblique cone with a diameter of 12 ft and a height of 15 ft. Before using the formula, we need to find the radius of the cone. 

radius = diameter/2 = 12/2 = 6

V_{oblique cone} = 1/3 × 3.14 × 6² × 15

V_{oblique cone} = 1/3 × 3.14 × 36 × 15

V_{oblique cone} = 1/3 × 3.14 × 540

V_{oblique cone} = 1/3 × 1695.6

V_{oblique cone} = 1/3 × 1695.6/1

V_{oblique cone} = (1 × 1695.6)/(3 × 1)

V_{oblique cone} = 1695.6/3

V_{oblique cone} = 565.2 ft³