Volume of a pyramid
The volume of a pyramid is how much space the pyramid occupies. We will start with a pyramid that has a square as the base. Look carefully at the pyramid shown below to see how the volume can be computed.
Volume of a pyramid formula
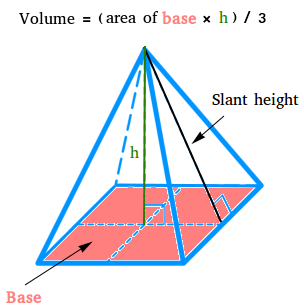
Suppose B is the area of the base, h is the height of the pyramid, and V is the volume.
Then, Volume = (B × h)/3 = Bh/3
In general, the volume of a pyramid is one third the product of the base area and the height of the pyramid.
The volume is expressed in cubic units.
- If the height h and the dimensions of the base are measured in centimeters or cm, then the volume is measured in cubic centimeters or cm3.
- If the height h and the dimensions of the base are measured in feet or ft, then the volume is measured in cubic feet or ft3.
- If the height h and the dimensions of the base are measured in inches, then the volume is measured in cubic inches or in.3.
There are different types of pyramids since the base of the pyramid can be a rectangle, a triangle, a square, or even a pentagon.
All you need to do is to compute the area of the base of the pyramid accordingly and then multiply by the height. In this lesson, you will learn how to compute the volume when the base is a square, a rectangle, or a triangle.
If you are dealing with a pyramid that has a pentagonal base or a hexagonal base, then check this lesson about area of a regular polygon to see how you can find the area.
How to calculate the volume of a pyramid with a square base.
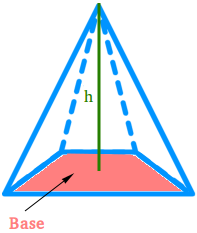
Example #1:
Find the volume of a square pyramid if the pyramid has a height of 9 meters and one side of the base measures 4 meters.
Since the base is a square, area of the base = 4 × 4 = 16 m2
Volume of the pyramid = (B × h)/3
Volume of the pyramid = (16 × 9)/3
Volume of the pyramid = 144/3 = 48 m3
How to calculate the volume of a pyramid with a rectangular base
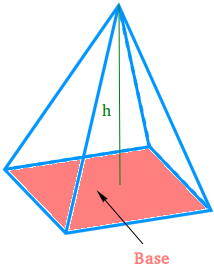
Example #2:
Find the volume of a rectangular pyramid if the pyramid has a height of 10 meters and the sides of the base measure 3 meters and 5 meters.
Since the base is a rectangle, area of the base = 3 × 5 = 15 m2
Volume of the pyramid = (B × h)/3
Volume of the pyramid = (15 × 10)/3
Volume of the pyramid = 150/3 = 50 m3
How to calculate the volume of a pyramid when the base is a triangle
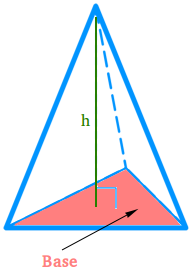
Example: #3
Find the volume of a triangular pyramid if the pyramid has a height of 8 meters and the triangular base has a base that is equal to 4 meters and a height that is equal to 3 meters.
Notice that here, you are dealing with two different heights. Avoid mixing the height of the pyramid with the height of the triangle.
Since the base is a triangle, area of the base = (b × h)/2 = (4 × 3)/2 = 12/2 = 6 m2.
Volume of the pyramid = (B × h)/3
Volume of the pyramid = (6 × 8)/3
Volume of the pyramid = 48/3
Volume of the pyramid = 16 m3
How to calculate the volume of a pyramid when the slant height is given
Example #4:
Find the volume of a square pyramid if one side of the base measures 40 meters and the pyramid has a slant height of 25 feet as shown below.

First, use the slanted height and the Pythagorean theorem to find the height h of the pyramid.
252 = 202 + h2
625 = 400 + h2
Subtract 400 from both sides of the equation
625 - 400 = 400 - 400 + h2
225 = h2
Solve for h by taking the square of both sides of the equation
√225 = √h2
h = 15
Then, find the volume of the pyramid
V = [(40×40)×15] / 3
V = (1600×15) / 3
V = (24000) / 3
V = 8000 ft3