|
 |
|||||
Volume of cylindersGiven the radius and h, the volume of cylinders can be found by using the formula: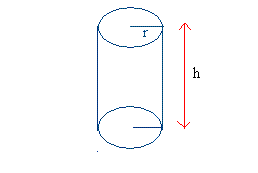  Volumecylinder = Area of base × height = pi × r2× h Use 3.14 for pi. Notice that the base of the cylinder is a circle and the formula to get the are is pi × r2 Example #1: Calculate Volumecylinder if r = 2 cm and h = 5 cm Volumecylinder = pi × r2× h Volumecylinder = 3.14 × 22× 5 Volumecylinder = 3.14 × 4 × 5 Volumecylinder = 3.14 × 20 Volumecylinder = 62.8 cm3 Example #2: Calculate Volumecylinder if r = 4 inches and h = 8 inches Volumecylinder = pi × r2× h Volumecylinder = 3.14 × 42× 8 Volumecylinder = 3.14 × 16 × 8 Volumecylinder = 3.14 × 128 Volumecylinder = 401.92 inches3 Fun game: Break spheres by matching balls with the same color
 |
|
|||||
|
IntroductionArithmeticGeometryGraph it!Probability and statisticsReal life mathSequences and patternsAlgebraResourcesTeachers!
Enjoy This Site?
Then why not use the button below, to add us to your favorite bookmarking service? |
||||||
| Powered by Site Build It | ||||||
|
| ||||||
