What is a normal distribution?
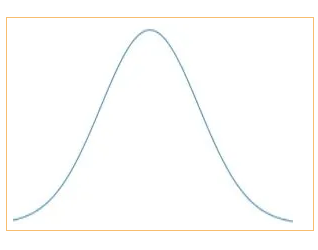
What is a normal distribution? The normal probability distribution, also called the normal curve, is given by a bell-shaped or symmetric curve such as the one you see in the figure below.
The normal probability distribution is one of the many probability distributions that a continuous random variable can have. Of all probability distributions, the normal probability distribution is the most important and most widely used.
Many situations that are observed in statistics are either normally distributed or approximately normally distributed.
A normal distribution can assume values that are infinite and uncountable. For example, the time it takes a student to commute from home to a university could be a normal distribution. Suppose that 15 minutes is the minimum time and 60 minutes is the maximum time it takes all students to commute from home to the university.
Let x be the time it takes a randomly selected student to commute from home to the university. Then, x can assume any value in the interval 15 to 60 minutes. This interval contains an infinite number of values that are uncountable.
To really understand what a normal distribution is, it is really important to understand what a continuous probability distribution is. In this unit, you will first learn about the probability distribution of continuous random variable. Then, the rest of the unit will focus on the normal distribution, which is in fact a specific case of continuous probability distribution. Do not miss the last topic in this unit about normal distribution word problems!