Why multiply before adding when doing PEMDAS?
Why multiply before adding when doing PEMDAS? It makes a lot of sense to multiply before adding when we follow the order of operations or PEMDAS. Keep reading and you will see why it is very important to follow this rule!
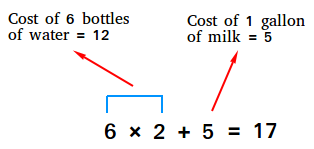
Say for example, you want to calculate 6 × 2 + 5 using the order of operations.
The order of operations tells us to multiply 6 and 2 first. However, the following question remains:
Why can't we add 2 and 5 first and then multiply the result by 6?
In order to see why it makes sense to multiply 6 and 2 first and then add 5 to the result, we need to turn the expression 6 × 2 + 5 into a word problem.
A nice word problem showing why multiply before adding is important when doing PEMDAS
Maria went to the supermarket and bought 6 bottles of water and 1 gallon of milk. If a bottle of water costs 2 dollars and a gallon of milk costs 5 dollars, how much money does she owe to the cashier?
The numerical expression for this word problem is 6 × 2 + 5.
Notice that if
you add 2 to 5 first and then multiply the result by 6, you will get 42
dollars. This does not make sense since that is way too much money for just 1
gallon of milk and 6 bottles of water. Let us find out what went wrong here!
After
adding 2 and 5, we get 7. However, 7 includes the price of 1 gallon of
water or 5 dollars. Therefore, if you multiply 7 by 6, you are in fact
multiplying the price of 1 gallon of milk or 5 by 6. In other words, this
means that you purchased 6 gallons of water or 6 × 5 = 30.
If indeed you did purchase 6 bottles of water and 6 gallons of milk, then the expression will look like this: 6 × (2 + 5)
Putting parentheses ensure that both 2 and 5 will be multiplied by 6. Without the parentheses or if the problem is 6 × 2 + 5, first you get the cost of buying 6 bottles of water and then add that to the cost of buying 1 gallon of milk.