30-60-90 triangle
A 30°-60-90 triangle is a special right triangle in which the length of the hypotenuse is twice the length of the shorter leg. The length of the longer leg is the square root of 3 times the length of the shorter leg.
Hypotenuse = 2 × shorter leg
Longer leg = √3 × shorter leg
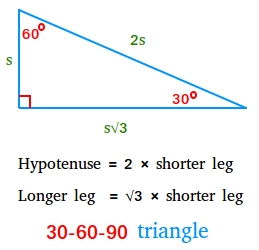
Looking carefully at the figure above, you may have observed the following ratios:
Suppose we start from the smallest angle to the largest angle and from the shortest side to the longest side
The angles of a 30-60-90 triangle are in the ratio 1:2:3
The sides of a 30-60-90 triangle are in the ratio 1:√3:2
30-60-90 triangle proof
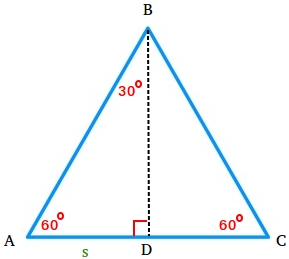
Start with an equilateral triangle ABC where each interior angle is equal to 60 degrees.
Since segment BD is the perpendicular bisector of segment AC, we now have two 30-60-90 triangles.
Let segment AD equal to s and use the Pythagorean theorem to find the length of segment BD.
Notice that AC = s + s = 2s. Since AB = AC, AB = 2s.
AD2 + BD2 = AB2
s2 + BD2 = (2s)2
s2 - s2 + BD2 = (2s)2 - s2
BD2 = (2s)2 - s2
BD2 = 4s2 - s2
BD2 = 3s2
BD = √(3s2)
BD = s√3
Examples of 30-60-90 triangles
Example #1: 1, √3, 2
Short leg: 1
long leg: √3
Hypotenuse: 2
Example #2: 2, 2√3, 4
Short leg: 2
long leg: 2√3
Hypotenuse: 4
Example #3: 5, 5√3, 10
Short leg: 5
long leg: 5√3
Hypotenuse: 10
Using the length of one side to solve a 30-60-90 triangle
Example #4:
The longer leg of a 30-60-90 triangle is 5. Find the lengths of the other sides.
Longer leg = √3 × shorter leg
5 = √3 × shorter leg
Shorter leg = 5/√3
Multiply both numerator and denominator of 5/√3 by √3
Shorter leg = 5(√3) / √3(√3)
Shorter leg = 5(√3) / √9
Shorter leg = 5(√3) / 3
Hypotenuse = 2 × shorter leg
Hypotenuse = 2 × [5(√3) / 3]
Hypotenuse = 10√3 / 3
Using the 30-60-90 triangle to solve real-world problems
Example #5:
The warning sign below is an equilateral triangle. Suppose the height of the sign is 1 meter. Find the length s of each side of the sign.

Since the triangle is an equilateral triangle, the altitude divides the triangle into two 30-60-90 triangles as shown in the figure below.
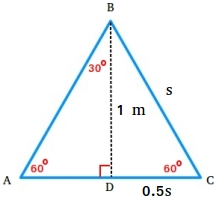
Notice that the length of the shorter leg is equal to (1/2)s or 0.5s since the altitude also bisects the base.
1 = √3 × shorter leg
1 = √3 × 0.5s
Divide both sides of the equation by 0.5
1/0.5 = (√3)s
2 = (√3)s
Divide both sides of the equation by (√3)
2/(√3) = s
s = 1.15 m
The length of each side of the sign is about 1.2 m
Example #6:
An escalator lifts people to the second floor, 40 feet above the first floor. The escalator rises at a 30 degrees angle. How far does the person travel from the bottom to the top of the escalator?
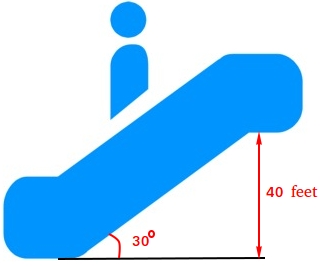
The figure above describes example #6 with a 30-60-90 triangle. Notice that the shorter side is 40 feet and it is opposite to the angle that measures 30 degrees.
The distance from the bottom of the escalator to the top is the length of the hypotenuse of the 30-60-90 triangle.
This distance is twice the length of the shorter side. Therefore, the distance you travel is 80 feet.
Area of a 30-60-90 triangle
To find the area of a 30-60-90 triangle, just make sure you get the height of the triangle correctly.
Keep in mind that either the longer side or the shorter side could be the height of the triangle. Just use the formula below:
Longer leg = √3 × shorter leg
If the shorter leg of the triangle is given, then the height = √3 × shorter leg and the shorter leg is the base.
If the longer leg of the triangle is given, then the height = longer leg / √3 and the base is the longer leg.
Example #7:
Find the area of the 30-60-90 triangle below
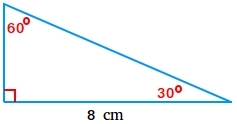
Since the longer leg is the base, height = 8/√3 = 4.618
Area = 8 × 4.618
Area = 36.944
The area of the triangle is 36.944 cm2