Using the 30-60-90 triangle to find sine and cosine

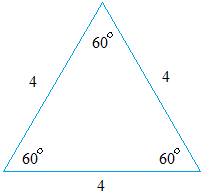
Before we can find the sine and cosine, we need to build our 30-60-90 degrees triangle. Start with an equilateral triangle with a side length of 4 like the one you see below.

Then, from one vertex, draw the line that is perpendicular to the side opposite the vertex. Notice that the black line bisect the side.

That is why the leg opposite the 30 degrees angle measures 2.

All we need to do is to find the length of the leg in black and we will be ready to find sin(30 degrees), sin(60 degrees), cos(30 degrees), and cos(60 degrees).

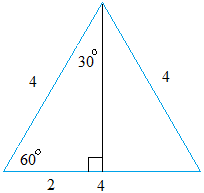
Call the length of the black line y and use the pythagorean theorem to find y.

4² = 2² + y²

16 = 4 + y²

16 - 4 = 4 - 4 + y²

12 = y²

y = √(12)

y = √(4 × 3)

y = √(4) × √(3)

y = 2√3

We pull out the right triangle and we are ready to find the trigonometric values of sine and cosine for this triangle.

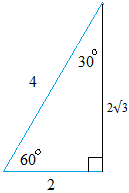
Important observation:

sin(60 degrees) = cos(30 degrees)

cos(60 degrees) = sin(30 degrees)

We will not do this computation, but if we replace 30 degrees with 20 degrees and 60 degrees with 70 degrees, you will find a similar result.

sin(70 degrees) = cos(20 degrees)

cos(70 degrees) = sin(20 degrees)

In general, 

sin(t) = cos(90 degrees - t)

cos(t) = sin(90 degrees - t)

We now have a couple more trigonometric formulas.