Approximating the area of a circle

Approximating the area of a circle using what we know about the area of a square is the method we are going to use here. Our technique is to inscribe a circle inside a square as shown below: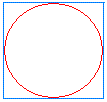
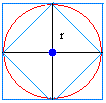
Then, inscribe a square inside the circle. Draw two diameters and they are shown in black
Label the radius and notice that the diameter of the circle is equal in length to the side of the big square.

To approximate the area of the circle, we will do the following:

1) Get area of the big square

2) Get the area of the small square

3) Take the average of answers found in 1) and 2)

1)

To get the area of the big square, notice that the length of the side of the big square is equal to r + r = 2r

Area = side × side

Area = 2r × 2r

Area = 4r²

2)

To get the area of the small square, find the area of one triangle inside that small square

Then, since 4 triangles make up the whole small square, just times the area of the triangle by 4

Notice also that the base = height = radius = r

Therefore,

Area of triangle = 1/2 × (r × r) = 1/2 × (r²)

Since there are 4 triangles, area of small square = 4 × 1/2(r²)

4 × 1/2(r²) = (4/1) × (1/2)× (r²)= 4/2 × (r²)= 2 × (r²)= 2(r²)

3)

Take the average of 4r² and 2 × (r²)

2(r²) + 4r² = 6r²

(6r²) / 2 = 3r²

So, the formula that estimate the area of a circle is 3r²

The exact formula is π × r² = 3.14 × r²

The formula 3r² is indeed a very good approximation

A little word problem about approximating the area of a circle

Approximate the area of a circle whose diameter is equal to 4 cm

The radius is half the diameter, so r = 2 cm

So an approximation of the area is 3r² = 3 × 2² = 3 × 4 = 12 cm ²