Area of triangles

This lesson will show you different ways to find the area of triangles. You could start by taking the quiz below to see how much you know. By definition, the area of a triangle is the amount of space taken by the triangle in a two-dimensional plane. 

Formula for Triangle Area:

A = 1/2 × base × height

Question 1 of 5

Area of a triangle formula

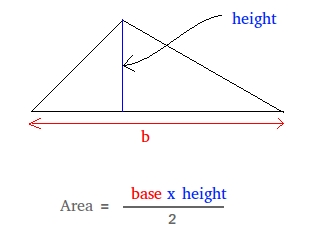
The most common way to find the area of a triangle is to use the basic formula shown below in blue. 

Area of a triangle = (base × height)/2

The red line represents the length of the base (call it b if you want) and the blue line represents the length of the height.

As you can see, to find the area, just multiply the base of the triangle by the height of the triangle and divide the result by 2. 

Area of a triangleArea of triangle

However, you can also find the area of a triangle based on the following two cases:

  • Three sides of the triangles are known (SSS triangle)
  • Two sides and the included angle are known (SAS triangle)

The area is expressed in square units.

  • If the base and the height are measured in meters, then the area is measured in square meters or m2.
  • If the base and the height are measured in centimeters, then the area is measured in square centimeters or cm2.

Examples showing how to find the area of triangles using the basic formula

Example #1

Find the area of the triangle shown in the figure below with base 9 inches and height 4 inches:

Base and height of a triangle

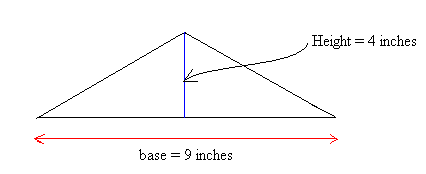
Area  = (base × height)/2

Area  = (9 × 4)/2

Area  = 36/2

Area  = 18

The area is 18 square inches or 18 in2

Example #2

Find the area of the obtuse triangle shown in the figure below with base 4 inches and height 3 inches:

Obtuse triangle with base of 4 inches and height 3 inches

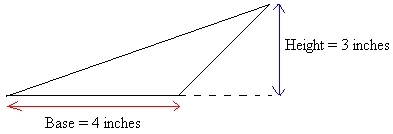
Area  = (base × height)/2

Area  = (4 × 3)/2

Area  = 12/2

Area  = 6

The area is 6 square inches or 6 in2

Example #3

Find the area of the right-angled triangle shown in the figure below with base 5 inches and height 6 inches:

Right-angled triangle with base 5 inches and height 6 inches

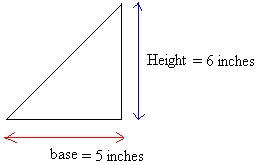
Area  = (base × height)/2

Area  = (5 × 6)/2

Area  = 30/2

Area  = 15

The area is 15 square inches or 15 in2

Using Heron's formula to find the area of a triangle when three sides of the triangle are known (SSS) 

The ancient Greek mathematician Heron is most famous for this formula for the area of a triangle when you know the lengths of its sides a, b, and c. 

The area is the square root of the product s(s-a)(s-b)(s-c).

A =√[s(s-a)(s-b)(s-c)], where s is the semi-perimeter of the triangle.

s = (a + b + c)/2

Example #4

The lengths of the sides of a triangle are 15 feet, 9 feet, and 12 feet. Use Heron's formula to find the area of the triangle.

s = (a + b + c)/2

s = (15 + 9 + 12)/2

s = (36)/2

s = 18

A =√[s(s-a)(s-b)(s-c)]

A =√[18(18-15)(18-9)(18-12)]

A =√[18(3)(9)(6)]

A =√[(54)(54)]

A =√(2916)

A = 54 square feet

Real the lesson about Heron's formula to see more examples.

Area of triangle when two sides and included angle are known (SAS)

When two sides and the angle between the two sides are known (SAS), the area is half the product of the adjacent sides times the sine of the included angle.

Therefore, use the formula below to find the area:

Area = [bc(sinA)]/2

Example #5

The lengths of two adjacent sides of a triangle are 8 cm and 12 cm. The angle between the sides is 60 degrees. Find the area of the triangle.

Let b = 8 cm, c = 12 cm, and A = 60 degrees

Area = [bc(sin A)]/2

Area = [8×12(sin 60 degrees)]/2

Area = [96(sin 60 degrees)]/2

Area = [96(0.866)]/2

Area = (83.136)/2

Area = 41.568 cm2

Real the lesson about area of a triangle given sas to see how the formula was derived and 1 more example showing how to use the formula.

Area of shapes

Area of an equilateral triangle