Area under the standard normal curve

Learn how to calculate the area under the standard normal curve. This is an important skill, so study the following examples carefully.

You will need the standard normal distribution table to solve problems. So go ahead and print the table and come back here.

Example #1

Find the area under the curve between z = 0 and z = 1.32

Looking at the table, we can see that 1.32 is no where to be found. However,  we can divide 1.32 into 1.3 and .02.

Locate 1.3 in the column for z on the left side of the table and locate .02 in the row for z at the top of the table. A portion of the table is reproduced below to show how to find the area.

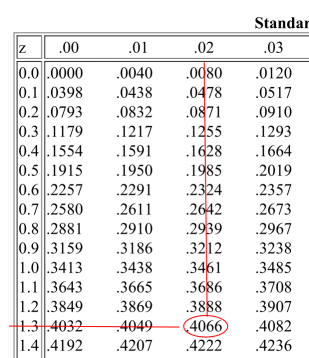
The area under the standard normal curve between 0 and 1.32 is 0.4066

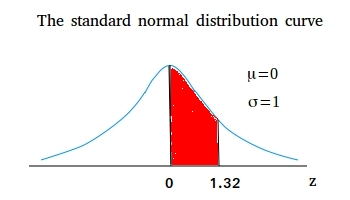
This area can be interpreted as the probability that z assumes a value between 0 and 1.32.

In other words, area between 0 and 1.32 = P (0 < z < 1.32) = 0.4066

Example #2

Find P(-1.32 < z < 0)

You just need to find the area under the normal curve between z = -1.32 and z = 0.

Because the normal curve is symmetric about the mean, the area from z = -1.32 to z  = 0 is the same as the area from z = 0 to z = 1.32.

This area was already calculated from example #1, so P(-1.32 < z < 0) = 0.4066

Example #3

Find the area under the standard normal curve to the right of z = 1.32

The area to the right of z = 1.32 is the area shaded in blue as shown below.

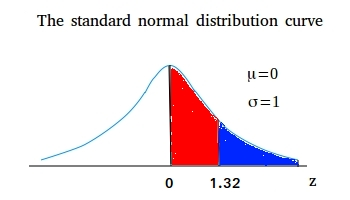
We also saw that in the lesson about standard normal distribution that the area in red plus the area in blue is equal to 0.5.

We already computed the area in red in example #1 and it is equal to 0.4066. Let x be the area in blue.

0.4066 + x = 0.5

x = 0.5 - 0.4066 = 0.0934

Example #4

Find the area between z = 1.32 and z  = 2.54

This area is shown in green. Notice that area from z = 0 to z = 1.32 plus area in green = area from z = 0 to z = 2.54

To find the area from z = 0 to z = 2.54, use the table to see that it is equal to .4945.

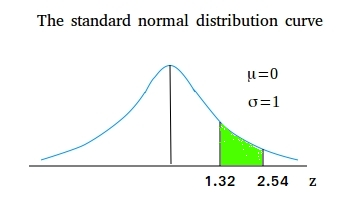
Area from z = 0 to z = 1.32 plus area in green = area from z = 0 to z = 2.54

Area from z = 0 to z = 1.32 is equal to 0.4066. Let x be the green area.

We get 0.4066 + x = 0.4945

x = 0.4945 - 0.4066 = 0.0879

Therefore, the area from z = 1.32 to z = 2.54 = 0.0879