Circumference of a Circle - Definition, Formula, and Examples
Circumference of a Circle Demonstration
What is the Circumference of a Circle?
The circumference of a circle, also called the perimeter of a circle, is the distance around a circle or any circular object such as a clock, a pizza, or a dinner plate. For example, the distance around a circular clock is the circumference of the clock.
How to Find the Circumference of a Circle?
Method 1:
You could use a flexible measuring tape like the one used in the image above to measure the perimeter of the clock. As you wrap the tape measure around the clock, just stretch the measuring tape as much as possible so the measurement can be as accurate as possible. Then, read the number you see on the measuring tape.
Method 2
Mark a point on the margin of any circular object. This is shown below with a vertical red mark. Roll the circular object either to the left or to the right until it makes one revolution. The distance between the vertical red marks is the circumference of the circular object.
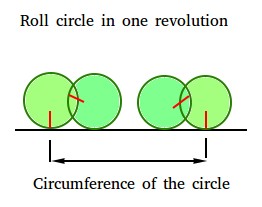
Method 3
Another way to find the perimeter of a circle or any circular object is to use a special formula.
Circumference formula
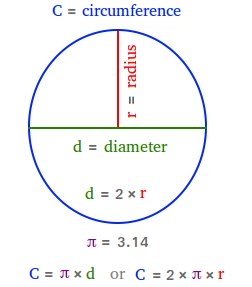
The perimeter of the circle can be found using either C = πd = π × d or C = 2 × π × r.
Pi or π is a special mathematical constant, and the value of pi is approximately equal to 22/7 or 3.14. The reason that we use 3.14 is because pi is an irrational number with unlimited digits after the decimal point. The lesson about the number π will tell you more about pi. It will also shows how to derive the formula and explain why the circle's circumference is C = π × d or C = 2 × π × r.
If either the radius of a circle (r) or the diameter of a circle (d) is known, you can find the circumference by simply substituting the known value for r or d in the formula.
The circumference is expressed in linear units.
- If r or d is measured in meters, then the circumference is also measured in meters or m.
- If r or d is measured in kilometers, then the circumference is measured in kilometers or km.
- If r or d is measured in inches, then the circumference is measured in inches or in.
How to find circumference of a circle using the diameter?
The product of the constant π and the diameter of the circle is equal to the circumference of the circle.
C = π × d
You just have to find the length of the diameter and them multiply by 3.14 to get the circumference. To get the diameter, use a ruler or a measuring tape. Measure from one edge of the circle to another edge making sure that you go through the midpoint or center of the circle (or clock). After I measured the diameter of the clock you see below, I found something close to 11.90 inches.
C = 3.14 × d = 3.14 × 11.9 = 37.36 inches. Looking at the measuring tape around the clock, we can see that the circumference is indeed close to 37.3 inches!
How to find circumference of a circle using the radius?
Twice the product of the constant π and the radius of the circle is equal to the circumference of the circle.
C = 2π × r
You just have to find the length of the radius r and them multiply by 2 and then by 3.14 to get the circumference. To get the radius, measure from the center of the circle(or clock) to the edge of the circle. After I measured the radius of the clock you see below, I found something close to 5.95 inches.
C = 2(3.14) × r = 2(3.14) × 5.95 = 37.36 inches. Again, looking at the measuring tape around the clock, we can see that the circumference is indeed close to 37.3 inches!
A few more Examples Showing how to Find the Circumference of a Circle
Examples #1Calculate the circumference of a circle if r = 2 inches
C = 2 × π × r = 2 × 3.14 × 2 = 12.56 inches
Examples #2
Calculate the circumference of a circle if r = 4 inches
C = 2 × π × r = 2 × 3.14 × 4 = 25.12 inches
Examples #3
If D = 10 centimeters, find the circumference.
You have two choices. You can first find r and then substitute its value for r in the formula.
r is half the diameter, so r = 10 divided by 2
r = 5 cm
C = 2 × π × r = 2 × 3.14 × 5 = 31.4 cm
Otherwise, you can just use the formula C = π × D
C = 3.14 × 10 = 31.4 cm
A Challenging Exercise about the Circumference of a Circle
Examples #4The circumference of circle A is four times the circumference of circle B
The diameter of circle B is 7. What is the diameter of circle A?
Let CA be the circumference of circle A
Let CB be the circumference of circle B
Let DA be the diameter of circle A
Let DB be the diameter of circle B
Since the ratio of circumference to diameter is the same for all circles, you can use the following proportion to solve this problem.
|
CA
DA
|
=
CB
DB
|
Things that we know:
CA = 4 × CB
DB = 7
Replace these in the proportion
|
4 × CB
DA
|
=
CB
7
|
28 × CB = DA × CB
Divide both sides by CB
DA = 28
|
CA
DA
|
=
CB
DB
|
Things that we know:
CA = 4 × CB
DB = 7
Replace these in the proportion
|
4 × CB
DA
|
=
CB
7
|
|
If
2
5
|
=
8
20
then, 2 × 20 = 5 × 8
|
|
If
4 × CB
DA
|
=
CB
7
|
Then, 4 × CB × 7 = DA × CB
28 × CB = DA × CB
Divide both sides by CB
DA = 28
How to Calculate the Circumference if the Area is Given
C = 2π × r
A = π × r2
Solve for r using A = πr2.
r2 = A/π
r = √(A/π)
Substitute √(A/π) for r in C
C = 2π × √(A/π)
C = 2√(π)2 × √(A/π)
C = 2√[(π)2 × (A/π)]
C = 2√[(π)×(A)]