Compound interest formula
A "simpler version" of the compound interest formula is A = P(1 + r)t and a more "complete version" is A = P(1 + r/n)nt
- A is the final balance, future value of the investment (FV), accumulated value, total amount accrued, etc...
- P is the principal, present value (PV), initial principal amount, initial amount, etc...
- r is the annual interest rate or rate of interest compounded once per year in the simpler version of the formula or more than once per year in the complete version of the formula. Keep in mind that r is compounded as a decimal.
- t is the time in years.
- n is the number of compounding periods or the number of times the interest is compounded (calculated and added to previous accumulated amount) each year.
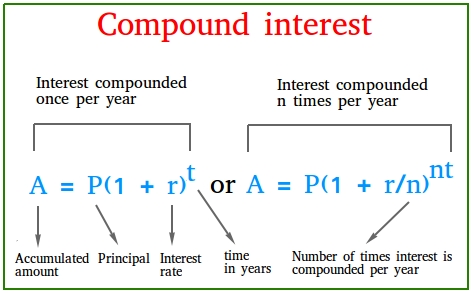
The principal is the amount of money you deposit that you expect will grow over time.
An example showing how to use the simpler version of the compound interest formula
Example #1
A businessperson invests 20000 dollars in a local bank paying 6% interest every year. How much money does the businessperson have in his account after 8 years?
Solution:
In this scenario, the interest rate r is compounded or "calculated and added to the account" only once per year. Therefore, you can just use the formula A = P(1 + r)t to find the accumulated amount after 8 years.
A = P(1 + r)t
A = 20000(1 + 6%)8
A = 20000(1 + 0.06)8
A = 20000(1.06)8
A = 2000(1.5938480)
A = 31,876.96
Many banks though have plans in which interest is paid more than once a year. The number of interest periods is the number of times the interest is computed and paid per year.
If the interest is computed and added to the account twice a year, this means that the number of interest periods is 2.
If the interest is computed and added to the account quarterly or four times a year, this means that the number of interest periods is 4.
Suppose the interest rate is 6% per year and the number of interest periods is 4. Then, each time the interest is compounded, the bank will use 6% / 4 or 1.5%.
In general, if r is the yearly interest and n is the number of interest periods in a year, each time the interest is compounded, the bank will use r / n.
The number of payment periods will also change. In the simpler version of the formula shown above, the number of payment periods is t. And t is the number of years.
Suppose each year though the interest is compounded 4 times. After 8 years, the number of payment periods is 4 × 8 or 32.
The number of payment periods is the total number of times interest is added to the account. In this case, it was done 32 times.
In general, if n is the number of interest periods in a year and t is the number of years, then the number of payment periods is n × t.
Therefore, a more complete version of the compound interest formula is:
A = P(1 + r / n)nt
How to use the more complete version of the compound interest formula
When using the formula A = P(1 + r/n)nt, keep in mind that the interest can be compounded daily, quarterly, triannually, semi-annually, twelve times a year(monthly), etc...
Example #2
Let us modify example #1 a little bit!
A businessperson invests 20000 dollars in a local bank paying 6% interest every year. The bank computes interest 4 times per year. How much money does the businessperson have in his account after 8 years?
Solution:
Now the interest rate is compounded or "calculated and added to the account" four times per year.
Therefore, you must use the formula A = P(1 + r / n)nt to find the accumulated amount after 8 years.
A = 20000(1 + r / n)nt
A = 20000(1 + 6% / 4)4×8
A = 20000(1 + 1.5%)32
A = 20000(1 + 0.015)32
A = 20000(1.015)32
A = 20000(1.61)
A = 32200
Notice that when the interest is paid 4 times a year, you end up with a little bit more money!
Annual compound interest formula
The annual compound interest formula is A = P(1 + r)t or the one I called "simpler version" of the compound interest formula.
It is called annual because of the fact that the interest is compounded annually or every year.
Daily compound interest formula
To calculate interest compounded daily, just use the daily compound interest formula
A = P(1 + r / 365)365t
In the formula, just divide the interest rate by 365 and multiply t or the number of years by 365.