Concave polygons

Concave polygons are polygons for which a line segment joining any two points in the interior does not lie completely within the figure.

The word interior is important. You cannot choose one point inside and one point outside the figure.

The following figure is concave:



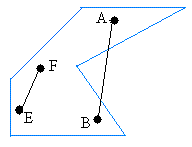
Segment AB does not entirely lie within the polygon. That is why the polygon is concave.

Notice that it is quite possible to find other segments that will lie inside the figure, such as segment FE.

However, if you can find at least one segment that does not lie within the figure, the figure is concave.

The following figure is also concave.




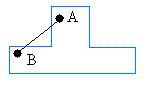
It is easy to construct a concave figure if the figure has at least 4 sides.

Just make sure that one interior angle is bigger than 180 degrees.

In other words, an interior angle should be a reflex angle.

Why am I saying at least 4 sides? Is it possible to make a concave triangle?

The answer is no!

Since the sum of the interior angles in any triangle must add up to 180 degrees, no interior angles can be more than 180. It is impossible!

There is another way to check if some polygons are concave polygons.

The second way to check if a polygon is a concave polygon is to look at the diagonals of the polygon.

If one or more diagonals are located outside or partly outside of the polygon, then the polygon is a concave polygon.

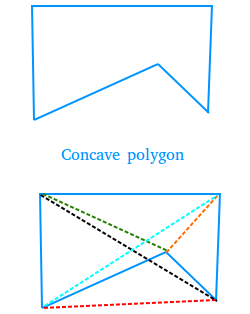
The polygon above has 5 diagonals made with dotted lines.

Three of them are completely inside and these are the green, orange, and teal dotted lines.

One is completely outside and it is red dotted line.

One is partially outside and it is the black dotted line.

The polygon is not a concave polygon because of the followings two situations occur.

• The black diagonal is partially located outside the polygon.
  
  
• The red diagonal is completely located outside the polygon.

A couple of exercises showing how to identify concave polygons by doing some math.

1. Four interior angles of an irregular pentagon measure 68, 176, 90 and 126. Is the irregular pentagon a concave pentagon? 

Solution

We just need to find the measure of the last angle to see if it is bigger than 180 degrees. The sum of the interior angles in a pentagon is 540.

68 + 176 + 90 + 126 + x = 540

460 + x = 540

x = 540 - 460 = 80

Since none of the angles inside the pentagon measure more than 180, the pentagon is not a concave pentagon.

2. Three interior angles of a quadrilateral measure 50, 105, and 15. Is the quadrilateral a concave quadrilateral? 

Solution

We just need to find the measure of the last angle to see if it is bigger than 180 degrees. The sum of the interior angles in a quadrilateral is 360.

50 + 105 + 15 + x = 360

170 + x = 360

x = 360 - 170 = 190

Since one angle inside the quadrilateral measure more than 180, the quadrilateral is a concave quadrilateral.