Convex polygons
Convex polygons are polygons for which a line segment joining any two points in the interior lies completely within the figure.
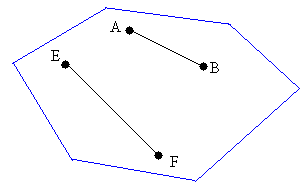
The word interior is important. You cannot choose one point inside and one point outside the figure.
The figure above with six sides meets this criteria and therefore is a convex polygon.
No matter how I choose two points inside this polygon, the line segment joining these two points will always be inside the figure.More examples of convex polygons
Notice that a triangle such as an isosceles triangle, a scalene triangle, a right triangle, or an obtuse triangle is always a convex polygon.
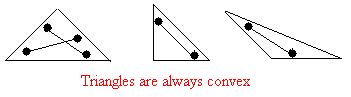
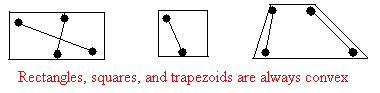
Rectangles, squares, and trapezoids too are always convex as well
Finally, all regular polygons, such as a pentagon, hexagon, septagon, octagon, and so forth are always convex
Buy a comprehensive geometric formulas ebook. All geometric formulas are explained with well selected word problems.
