Conditional probability
A conditional probability contains a condition which forces you to focus your attention to a subset of the sample space. For example, a company may have males and females working for the company. However, you may want to answer questions about males only or females only. If you are dealing with insurance, you may want to answer questions about smokers only or non-smokers only.
A good way to get started with conditional probabilities is to use a contingency table.
Conditional probability using a contingency table
Here is how to find the conditional probability using a contingency table that we used in the lesson about marginal probability. The table shows test results for 200 students who took a GED test.
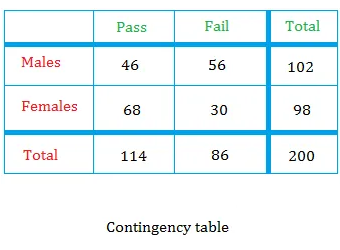
From the list of 200 students, we select a student randomly. However, suppose that you already know the student selected is a male.
The fact that you know the student is a male means that the event has already occurred. And it forces you to focus your attention only on males or 102 possible outcomes.
What is conditional probability?
Knowing that the student is a male, you can calculate the probability that this student has passed or failed. This kind of probability is called conditional probability
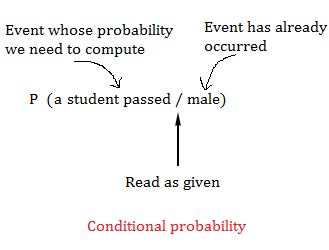
The notation to find the probability that 'a student has passed if the student is male is
P(a student has passed / male)
You could in fact compute any of the following 8 conditional probabilities:
- P(a student has passed / male)
- P(a student has passed / female)
- P(a student has failed / male)
- P(a student has failed / female)
- P(a student is male / passed)
- P(a student is male / failed)
- P(a student is female / passed)
- P(a student is female / failed)
A couple of examples showing how to find the conditional probability using a contingency table
Example #1
Let us compute the P(a student has passed / male).
If the student is male, then the student will be picked from the list of 102 males.
From this list only 46 students have passed.

Example #2
What about P(a student is male / passed) ?
The number of students who passed is equal to 114.
From this list, only 46 students are males.
As you can see from the results P(a student has passed / male) is not equal to
P(a student is male / passed) because there is a difference.
P(a student has passed / male): This probability just shows the success rate of males only.
P(a student is male / passed): This probability compares the success rate of males to females.
Conditional probability formula
Take a close look again at the following ratio:
Let M be the event 'the student is a male'
Let P be the event 'the student has passed'
Let P∩M be the event 'the student is a male and has passed'
n(P∩M) = number of male students who passed = 46
n(M) = total number of male students = 102
We can get the same answer using probability instead of counting. Divide the numerator and the denominator of the ratio immediately above by 200.
P(P∩M) = probability that a student has passed if the student is male = 46 / 200 = 0.23
P(M) = probability that a student is male = 102 / 200 = 0.51
We can then conclude that there are two ways to find a conditional probability.
How to find the conditional probability by counting
If you are dealing with equally likely outcomes such as tossing a coin or a fair die with six sides, then for any two events A and B, you can use the following formula:
How to find the conditional probability by using the definition of conditional probability
Whether you are dealing with equally likely outcomes or not, then for any two events A and B, you can use the following formula:
The probability of A given B is the ratio of the probability of the intersection of A and B to the probability of B.
More examples of conditional probability
Example #3
A card is drawn at random from a standard deck. The card is not replaced. Find the probability that the second card is a king given that the first card drawn was a king.
Let K1 be event 'the first card drawn is a king' and K2 be the event 'the second card drawn is a king'
If a king is drawn and not replaced, then there are 3 kings left and the deck will now have 51 cards.
P(K2 / K1) = 3/51 ≈ 0.0588
Two events A and B are called independent events if P(A / B) = P(A)
Example #4
Let H1 be the event that the first toss of a coin is a head and let H2 be the event that the second toss of the coin is a head. Show that H1 and H2 are independent events.
Your calculations must show that P(H2 / H1) = P(H2)
The full sample space is {HH, HT, TH, TT}
H2 = {HH, TH} and P(H2) = 0.50
Given that the first toss is a head, we end up with {HH, HT} and we are restricted to these two outcomes to compute P(H2 / H1)
From these two outcomes, we see that HH (half of the 2 outcomes) has a head as the second toss.
P(H2 / H1) = 0.5
P(H2 / H1) = P(H2) = 0.5, and thus H1 and H2 are independent events.
In independent events, the occurrence of an event does not influence the occurrence of another event. In example #4, the event 'you get a head with the first toss or H1' will not influence the likelihood of getting again a head with the second toss.
This is not the case with example #3 where the occurrence of an event can influence the occurrence of another.
Two events A and B are called dependent events if P(A / B) ≠ P(A)
In example #3, P(K2 / K1) = 3/51. However, P(K2) = 4/52 = 0.076
Since the first card was not replaced or put back in the deck, the probability of the second draw clearly depends on the outcome of the first,