Division of Integers
Division of integers is the opposite operation of multiplying integers. It is the process by which one is trying to determine how many times a number is contained into another.
Say for instance you do 42 ÷ 6 as shown in the figure below. You are trying to find out how many times 6 is contained into 42.
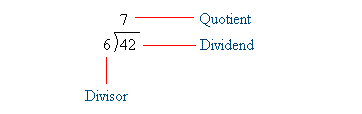
Since 6 × 7 = 42, 6 is contained into 42 seven times. Thus, 42 ÷ 6 = 7
Now, it is very important to make the following observations:
quotient × divisor = dividend
dividend ÷ divisor = quotient
dividend ÷ quotient = divisor
In other words, if the product of 4 × 5 = 20, then dividing the product, which is 20 by 4 gives you back 5.
By the same token, dividing the product or 20 by 5 gives you back 4. Having said that, we can use this fact to find the rule for dividing integers.
Now, let us see why the rule above makes sense. Since we know that 2 × 6 = 12, then 12 ÷ 6 = 2.
12, 6, and 2 are positive, so we can conclude the following:
positive ÷ positive = positive
Since we know that 2 × -6 = -12, then -12 ÷ -6 = 2.
-12 and -6, are negative, but 2 is positive, so we can conclude the following:
negative ÷ negative = positive
In our previous example, notice also that -12 ÷ 2 = -6
-12 is negative, 2 is positive, and -6 is negative, so we can conclude the following:
negative ÷ positive = negative
Finally, consider -2 × -6 = 12
Then, 12 ÷ -2 = -6
12 is positive, -2 is negative, and -6 is negative, so we can conclude the following:
positive ÷ negative = negative
Notice also that the rule for division of integers is the same for multiplying integers. Therefore, if you remember the rule for multiplying integers, you already know it for division.
In a nutshell, here is the most important stuff that you need to remember from this lesson about division of integers:
The division of two integers with the same signs is positive
The division of two integers with different signs is negative
Need a little bit more help in order to understand the rule above about division of integers? Here is a summary!
